travelling salesman problem dataset

• Google OR-Tools
• Español – América Latina
• Português – Brasil
• Tiếng Việt

Traveling Salesperson Problem

This section presents an example that shows how to solve the Traveling Salesperson Problem (TSP) for the locations shown on the map below.

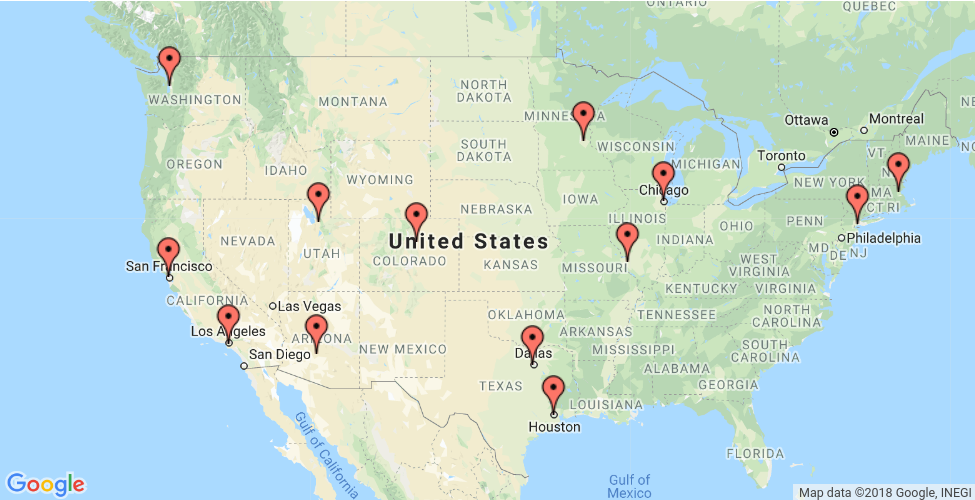
The following sections present programs in Python, C++, Java, and C# that solve the TSP using OR-Tools

Create the data

The code below creates the data for the problem.

The distance matrix is an array whose i , j entry is the distance from location i to location j in miles, where the array indices correspond to the locations in the following order:

The data also includes:

• The number of vehicles in the problem, which is 1 because this is a TSP. (For a vehicle routing problem (VRP), the number of vehicles can be greater than 1.)
• The depot : the start and end location for the route. In this case, the depot is 0, which corresponds to New York.

Other ways to create the distance matrix

In this example, the distance matrix is explicitly defined in the program. It's also possible to use a function to calculate distances between locations: for example, the Euclidean formula for the distance between points in the plane. However, it's still more efficient to pre-compute all the distances between locations and store them in a matrix, rather than compute them at run time. See Example: drilling a circuit board for an example that creates the distance matrix this way.

Another alternative is to use the Google Maps Distance Matrix API to dynamically create a distance (or travel time) matrix for a routing problem.

Create the routing model

The following code in the main section of the programs creates the index manager ( manager ) and the routing model ( routing ). The method manager.IndexToNode converts the solver's internal indices (which you can safely ignore) to the numbers for locations. Location numbers correspond to the indices for the distance matrix.

The inputs to RoutingIndexManager are:

• The number of rows of the distance matrix, which is the number of locations (including the depot).
• The number of vehicles in the problem.
• The node corresponding to the depot.

Create the distance callback

To use the routing solver, you need to create a distance (or transit) callback : a function that takes any pair of locations and returns the distance between them. The easiest way to do this is using the distance matrix.

The following function creates the callback and registers it with the solver as transit_callback_index .

The callback accepts two indices , from_index and to_index , and returns the corresponding entry of the distance matrix .

Set the cost of travel

The arc cost evaluator tells the solver how to calculate the cost of travel between any two locations — in other words , the cost of the edge ( or arc ) joining them in the graph for the problem . The following code sets the arc cost evaluator .

In this example, the arc cost evaluator is the transit_callback_index , which is the solver's internal reference to the distance callback. This means that the cost of travel between any two locations is just the distance between them. However, in general the costs can involve other factors as well.

You can also define multiple arc cost evaluators that depend on which vehicle is traveling between locations, using the method routing.SetArcCostEvaluatorOfVehicle() . For example, if the vehicles have different speeds, you could define the cost of travel between locations to be the distance divided by the vehicle's speed — in other words, the travel time.

Set search parameters

The following code sets the default search parameters and a heuristic method for finding the first solution:

The code sets the first solution strategy to PATH_CHEAPEST_ARC , which creates an initial route for the solver by repeatedly adding edges with the least weight that don't lead to a previously visited node (other than the depot). For other options, see First solution strategy .

Add the solution printer

The function that displays the solution returned by the solver is shown below. The function extracts the route from the solution and prints it to the console.

The function displays the optimal route and its distance, which is given by ObjectiveValue() .

Solve and print the solution

Finally, you can call the solver and print the solution:

This returns the solution and displays the optimal route.

Run the programs

When you run the programs, they display the following output.

In this example, there's only one route because it's a TSP. But in more general vehicle routing problems, the solution contains multiple routes.

Save routes to a list or array

As an alternative to printing the solution directly, you can save the route (or routes, for a VRP) to a list or array. This has the advantage of making the routes available in case you want to do something with them later. For example, you could run the program several times with different parameters and save the routes in the returned solutions to a file for comparison.

The following functions save the routes in the solution to any VRP (possibly with multiple vehicles) as a list (Python) or an array (C++).

You can use these functions to get the routes in any of the VRP examples in the Routing section.

The following code displays the routes.

For the current example, this code returns the following route:

As an exercise, modify the code above to format the output the same way as the solution printer for the program.

Complete programs

The complete TSP programs are shown below.

Example: drilling a circuit board

The next example involves drilling holes in a circuit board with an automated drill. The problem is to find the shortest route for the drill to take on the board in order to drill all of the required holes. The example is taken from TSPLIB, a library of TSP problems.

Here's scatter chart of the locations for the holes:

The following sections present programs that find a good solution to the circuit board problem, using the solver's default search parameters. After that, we'll show how to find a better solution by changing the search strategy .

The data for the problem consist of 280 points in the plane, shown in the scatter chart above. The program creates the data in an array of ordered pairs corresponding to the points in the plane, as shown below.

Compute the distance matrix

The function below computes the Euclidean distance between any two points in the data and stores it in an array. Because the routing solver works over the integers, the function rounds the computed distances to integers. Rounding doesn't affect the solution in this example, but might in other cases. See Scaling the distance matrix for a way to avoid possible rounding issues.

Add the distance callback

The code that creates the distance callback is almost the same as in the previous example. However, in this case the program calls the function that computes the distance matrix before adding the callback.

Solution printer

The following function prints the solution to the console. To keep the output more compact, the function displays just the indices of the locations in the route.

Main function

The main function is essentially the same as the one in the previous example , but also includes a call to the function that creates the distance matrix.

Running the program

The complete programs are shown in the next section . When you run the program, it displays the following route:

Here's a graph of the corresponding route:

The OR-Tools library finds the above tour very quickly: in less than a second on a typical computer. The total length of the above tour is 2790.

Here are the complete programs for the circuit board example.

Changing the search strategy

The routing solver does not always return the optimal solution to a TSP, because routing problems are computationally intractable. For instance, the solution returned in the previous example is not the optimal route.

To find a better solution, you can use a more advanced search strategy, called guided local search , which enables the solver to escape a local minimum — a solution that is shorter than all nearby routes, but which is not the global minimum. After moving away from the local minimum, the solver continues the search.

The examples below show how to set a guided local search for the circuit board example.

For other local search strategies, see Local search options .

The examples above also enable logging for the search. While logging isn't required, it can be useful for debugging.

When you run the program after making the changes shown above, you get the following solution, which is shorter than the solution shown in the previous section .

For more search options, see Routing Options .

The best algorithms can now routinely solve TSP instances with tens of thousands of nodes. (The record at the time of writing is the pla85900 instance in TSPLIB, a VLSI application with 85,900 nodes. For certain instances with millions of nodes, solutions have been found guaranteed to be within 1% of an optimal tour.)

Scaling the distance matrix

Since the routing solver works over the integers, if your distance matrix has non-integer entries, you have to round the distances to integers. If some distances are small, rounding can affect the solution.

To avoid any issue with rounding, you can scale the distance matrix: multiply all entries of the matrix by a large number — say 100. This multiplies the length of any route by a factor of 100, but it doesn't change the solution. The advantage is that now when you round the matrix entries, the rounding amount (which is at most 0.5), is very small compared to the distances, so it won't affect the solution significantly.

If you scale the distance matrix, you also need to change the solution printer to divide the scaled route lengths by the scaling factor, so that it displays the unscaled distances of the routes.

Except as otherwise noted, the content of this page is licensed under the Creative Commons Attribution 4.0 License , and code samples are licensed under the Apache 2.0 License . For details, see the Google Developers Site Policies . Java is a registered trademark of Oracle and/or its affiliates.

Last updated 2024-08-28 UTC.

• Interview Problems on Graph
• Practice Graph
• MCQs on Graph
• Graph Tutorial
• Graph Representation
• Graph Properties
• Types of Graphs
• Graph Applications
• BFS on Graph
• DFS on Graph
• Graph VS Tree
• Transpose Graph
• Dijkstra's Algorithm
• Minimum Spanning Tree
• Prim’s Algorithm
• Topological Sorting
• Floyd Warshall Algorithm
• Strongly Connected Components
• Advantages & Disadvantages

Traveling Salesman Problem (TSP) Implementation

Travelling Salesman Problem (TSP) : Given a set of cities and distances between every pair of cities, the problem is to find the shortest possible route that visits every city exactly once and returns to the starting point.  Note the difference between Hamiltonian Cycle and TSP. The Hamiltonian cycle problem is to find if there exists a tour that visits every city exactly once. Here we know that Hamiltonian Tour exists (because the graph is complete) and in fact, many such tours exist, the problem is to find a minimum weight Hamiltonian Cycle.  For example, consider the graph shown in the figure on the right side. A TSP tour in the graph is 1-2-4-3-1. The cost of the tour is 10+25+30+15 which is 80. The problem is a famous NP-hard problem. There is no polynomial-time known solution for this problem.   

Examples: 

In this post, the implementation of a simple solution is discussed.

• Consider city 1 as the starting and ending point. Since the route is cyclic, we can consider any point as a starting point.
• Generate all (n-1)! permutations of cities.
• Calculate the cost of every permutation and keep track of the minimum cost permutation.
• Return the permutation with minimum cost.

Below is the implementation of the above idea 

Time complexity:  O(n!) where n is the number of vertices in the graph. This is because the algorithm uses the next_permutation function which generates all the possible permutations of the vertex set.  Auxiliary Space: O(n) as we are using a vector to store all the vertices.

Please Login to comment...

Similar reads.

• NP Complete
• Discord Emojis List 2024: Copy and Paste
• Best Adblockers for Twitch TV: Enjoy Ad-Free Streaming in 2024
• PS4 vs. PS5: Which PlayStation Should You Buy in 2024?
• Best Mobile Game Controllers in 2024: Top Picks for iPhone and Android
• System Design Netflix | A Complete Architecture

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Traveling Salesman Algorithms

From naive to christofide, how to read this article.

Our article was written using a component-based library called Idyll. In addition to buttons and sliders you will see the following in this article... This component is an external link which will redirect you to another page. This component is an internal link which will send you to a part of the page when clicked on. This component is an action link which will trigger some event on the page to do something. Lastly, this article is only supported on Chrome; other browsers have an SVG rendering bug that can show up.

Introduction

Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city exactly once and returns to the origin city?

In essence, this question is asking us (the salesman) to visit each of the cities via the shortest path that gets us back to our origin city. We can conceptualize the TSP as a graph where each city is a node, each node has an edge to every other node, and each edge weight is the distance between those two nodes.

The first computer coded solution of TSP by Dantzig, Fulkerson, and Johnson came in the mid 1950’s with a total of 49 cities. Since then, there have been many algorithmic iterations and 50 years later, the TSP problem has been successfully solved with a node size of 24,978 cities! Multiple variations on the problem have been developed as well, such as mTSP , a generalized version of the problem and Metric TSP , a subcase of the problem.

The original Traveling Salesman Problem is one of the fundamental problems in the study of combinatorial optimization—or in plain English: finding the best solution to a problem from a finite set of possible solutions . This field has become especially important in terms of computer science, as it incorporate key principles ranging from searching, to sorting, to graph theory.

Real World Applications

However, before we dive into the nitty gritty details of TSP, we would like to present some real-world examples of the problem to illustrate its importance and underlying concepts. Applications of the TSP include:

Click on an example to the left for more information!

• Santa delivering presents.
• Fulfilling an order in a warehouse.
• Designing and building printed circuit boards.
• Analyzing an X-Ray.
• GPS satellite systems.
• School bus scheduling.

Finding Solutions – Exact vs. Approximation

The difficulty in solving a combinatorial optimization problem such as the TSP lies not in discovering a single solution, but rather quickly verifying that a given solution is the optimal solution. To verify, without a shadow of a doubt, that a single solution is optimized requires both computing all the possible solutions and then comparing your solution to each of them. We will call this solution the Exact solution. The number of computations required to calculate this Exact solution grows at an enormous rate as the number of cities grow as well. For example, the total number of possible paths for 7 cities is just over 5,000 , for 10 cities it is over 3.6 million , and for 13 cities it is over 6 billion . Clearly, this growth rate quickly eclipses the capabilities of modern personal computers and determining an exact solution may be near impossible for a dataset with even 20 cities. We will explore the exact solution approach in greater detail during the Naïve section.

The physical limitations of finding an exact solution lead us towards a very important concept – approximation algorithms . In an approximation algorithm, we cannot guarantee that the solution is the optimal one, but we can guarantee that it falls within a certain proportion of the optimal solution. The real strength of approximation algorithms is their ability to compute this bounded solution in an amount of time that is several orders of magnitude quicker than the exact solution approach. Later on in this article we will explore two different approximation algorithms, Nearest Neighbor and Christofide’s Algorithm , and the many facets of each approach.

The Naïve Approach

We can imagine that from a starting city, there are ∣ V ∣ − 1 |V| - 1 ∣ V ∣ − 1 possibilities for the second city. Following this connection, the second city will then have ∣ V ∣ − 2 |V| - 2 ∣ V ∣ − 2 possibilities, and so on and so on... Since our path is bidirectional, it follows that some cycles we calculate at will be disposible as they are duplicates if reversed. Thus we arrive at ( ∣ V ∣ − 1 ) ! / 2 (|V| - 1)!/2 ( ∣ V ∣ − 1 ) ! / 2 possible paths.

This figure can better be expressed as having a bound O ( ∣ V ∣ ! ) O(|V|!) O ( ∣ V ∣ ! ) possible paths. As explored above, a factorial upper bound is simply far too great for real applications.

Nearest Neighbor

Choose the next city in the path to be the closest city that you have not already visited. Once all cities have been visited, the salesman return home.

Next: Click here for a quick walkthrough of the algorithm!

Christofides Algorithm

Steps: Intro MST Odd Vertices Matches Eulerian Hamiltonian

This section is meant to serve as a “slide show” that will walk you through the previously outlined 5 steps of Christofides’ Algorithm. At each step after this one you will be able to switch between a Small Dataset , Medium Dataset , and Large Dataset , Clear the edges in the graph, and move to the previous step and Next Step in the algorithm.

In addition, each step can be accessed by clicking its corresponding button underneath the map to the right. Next Step: Minimum Spanning Tree

Algorithm Analysis

While the Naïve and dynamic programming approaches always calculate the exact solution, it comes at the cost of enormous runtime; datasets beyond 15 vertices are too large for personal computers. The most common approximation algorithm, Nearest Neighbor, can produce a very good result (within 25% of the exact solution) for most cases, however it has no guarantee on its error bound. That said, Christofides algorithm has the current best error bound of within 50% of the exact solution for approximation algorithms. Christofides produces this result in a “good” runtime compared to Naïve and dynamic, but it still significantly slower than the Nearest Neighbor approach.

In the chart above the runtimes of the naive, dynamic programming, nearest neighbors, and Christofides’ are plotted. The x-axis represents the number of cities that the algorithm works on while the y-axis represents the worst-case amount of calculations it will need to make to get a solution. As you can see, as the number of cities increases every algorithm has to do more calculations however naive will end up doing significantly more. Note how with 20 cities, the naive algorithm is 5,800,490,399 times slower than even the minimally faster dynamic programming algorithm.

Closing Thoughts

We would like to thank Dr. Heer, Matthew Conlen, Younghoon Kim, and Kaitlyn Zhou for their contributions to CSE 442, the UW Interactive Data Lab, Idyll, and much more. This article would not have been possible without their support and guidance.

Sources, References, and Links:

Inspiration from Idyll articles: Flight, Barnes Hut

• Prospective Students
• Current Students
• Teaching Staff
• Lifelong learning
• All Degree Programs
• ALMA Portal
• Excellence Strategy
• Staff Search (EPV)
• Student Administration
• University Library
• Online Course Catalogue
• Webmail Uni Tübingen
• Advice for International Students

Traveling Salesperson Problem Dataset

With our game "Perlentaucher" (in German, but playable for everyone), we observe how players solve different variants of the Traveling Salesperson problem.

The original Perlentaucher 1 replicates some TSP instances from the literature and includes some randomly generated tasks. It also varies whether the starting node is predefined and whether points are visually marked with different colors. It contains 24 levels (= TSP instances).

The sequel Perlentaucher 2 contains levels to validate our model of choosing start nodes, but can also be used for other research questions. It contains 90 levels.

Further Information

Modeling Human Problem Solving with Data from an Online Game (Tim Rach, Alexandra Kirsch), In Cognitive Processing 17(4), 2016 , doi:10.1007/s10339-016-0767-4.

• Poster presented at Dagstuhl Seminar "Resource-bounded Problem Solving", 2014

TSP Data for the Traveling Salesperson Problem

TSP is a dataset directory which contains some examples of data for the traveleing salesperson problem.

Most of these examples come from TSPLIB, a collection of traveling salesman problem datasets maintained by Gerhard Reinelt at "http://comopt.ifi.uni-heidelberg.de/software/TSPLIB95/"

In the traveling salesperson problem, a salesperson, who lives in one of the cities, is expected to make a round trip visiting all the other cities and returning home. (It doesn't actually matter which city is the starting point.) The requirement is that the total distance traveled be as small as possible.

It turns out that this simple problem is actually remarkably hard to solve, particularly if one insists on finding the absolutely best answer. Approaches to solving this problem have used simple enumeration, Monte Carlo estimation, minimal spanning trees, linear programming, simulated annealing, Tabu searches, the branch and bound procedure, the integer assignment problem, the convex hull, genetic algorithms, ant colony algorithms, and the cross-entropy method,

Thus, this simple problem has been the inspiration for many new ways of trying to solve not just the traveling salesperson problem but related "combinatorial optimization" problems, in which a discrete set of choices result in a payoff which is to be maximized or a cost which is to be minimized.

In the simplest version of the traveling salesperson problem, it is possible to travel from any city A to any city B, and the distance is the same both ways. This might be imagined to correspond to travel by air.

In a variation of the problem, it might not be possible to travel directly between certain cities. This is essentially equivalent to setting the corresponding intercity distance to be infinite. This could be considered an attempt to include the realities of highway travel.

To specify the problem, we may provide the spatial coordinates of the N points. Here again, there can be complications. It would be natural to expect coordinates on a plane, with the Euclidean distance, but the data might be more accurately described as lying on a sphere, with travel constrained to the surface; or we might have locations in a gridded city, in which case distance is measured with the L1 norm rather than the Euclidean norm, and there are further obvious variations.

If we are given a set of coordinates and a description of the distance function, we can compute the distance matrix. So we might suppose that any distance matrix comes from a set of point coordinates. But that's not true. If we start with the distance matrix, we are free to put down numbers that violate the triangle inequality, for instance. Problems in which the data does not come from an underlying set of point coordinates and a norm turn out to be much harder, since certain geometric facts can no longer be used to estimate the solution.

For the data considered here, we will expect symmetry, that is, that the distance is the same coming and going. We will allow problems to be specified either by node coordinates and a norm, (usually 2D planar points and the Euclidean norm) or by an abstract distance matrix.

The computer code and data files described and made available on this web page are distributed under the GNU LGPL license.

Related Data and Programs:

CITIES , a dataset directory which contains sets of information about cities and the distances between them;

CITIES , a FORTRAN90 library which handles various problems associated with a set of "cities" on a map.

CITIES , a MATLAB library which handles various problems associated with a set of "cities" on a map.

DISTANCE_TO_POSITION , a FORTRAN90 program which estimates the positions of cities based on a city-to-city distance table.

DISTANCE_TO_POSITION , a MATLAB program which estimates the positions of cities based on a city-to-city distance table.

DISTANCE_TO_POSITION_SPHERE , a MATLAB program which estimates the positions of cities on a sphere (such as the earth) based on a city-to-city distance table.

LAU_NP , a FORTRAN90 library which implements heuristic algorithms for various NP-hard combinatorial problems.

• Gerhard Reinelt, TSPLIB - A Traveling Salesman Problem Library, ORSA Journal on Computing, Volume 3, Number 4, Fall 1991, pages 376-384.
• att48.tsp , the TSP specification of the data.
• att48_d.txt , the intercity distance table.
• att48_xy.txt , the xy coordinates of each city.
• att48_s.txt , an itinerary that minimizes the total distance.
• dantzig42.tsp , the TSP specification of the data.
• dantzig42_d.txt , the intercity distance table.
• fri26.tsp , the TSP specification of the data.
• fri26_d.txt , the intercity distance table.
• fri26_s.txt , an itinerary that minimizes the total distance.
• gr17.tsp , the TSP specification of the data.
• gr17_d.txt , the intercity distance table.
• gr17_s.txt , an itinerary that minimizes the total distance (not available yet).
• p01.tsp , the TSP specification of the data.
• p01_d.txt , the intercity distance table.
• p01_s.txt , an itinerary that minimizes the total distance.
• p01_sxy.txt , the XY coordinates of the minimal itinerary.DFRAP
• p01_sxy.png , an image of the minimal itinerary.
• p01_xy.txt , a set of XY coordinates for the cities, inferred from the distances.
• p01_xy.png , an image of the XY coordinates.

You can go up one level to the DATASETS directory .

Navigation Menu

Search code, repositories, users, issues, pull requests..., provide feedback.

We read every piece of feedback, and take your input very seriously.

Saved searches

Use saved searches to filter your results more quickly.

To see all available qualifiers, see our documentation .

• Notifications You must be signed in to change notification settings

Code for the paper 'An Efficient Graph Convolutional Network Technique for the Travelling Salesman Problem' (INFORMS Annual Meeting Session 2019)

chaitjo/graph-convnet-tsp

Folders and files, repository files navigation, an efficient graph convolutional network technique for the travelling salesman problem.

🚀 Update: If you are interested in this work, you may be interested in our latest paper and up-to-date codebase bringing together several architectures and learning paradigms for learning-driven TSP solvers under one pipeline.

This repository contains code for the paper "An Efficient Graph Convolutional Network Technique for the Travelling Salesman Problem" by Chaitanya K. Joshi, Thomas Laurent and Xavier Bresson.

We introduce a new learning-based approach for approximately solving the Travelling Salesman Problem on 2D Euclidean graphs. We use deep Graph Convolutional Networks to build efficient TSP graph representations and output tours in a non-autoregressive manner via highly parallelized beam search. Our approach outperforms all recently proposed autoregressive deep learning techniques in terms of solution quality, inference speed and sample efficiency for problem instances of fixed graph sizes.

The notebook main.ipynb contains top-level methods to reproduce our experiments or train models for TSP from scratch. Several modes are provided:

• Notebook Mode : For debugging as a Jupyter Notebook
• Visualization Mode : For visualization and evaluation of saved model checkpoints (in a Jupyter Notebook)
• Script Mode : For running full experiments as a python script

Configuration parameters for notebooks and scripts are passed as .json files and are documented in config.py .

Pre-requisite Downloads

Tsp datasets.

Download TSP datasets from this link : Extract the .tar.gz file and place each .txt file in the /data directory. (We provide TSP10, TSP20, TSP30, TSP50 and TSP100.)

Pre-trained Models

Download pre-trained model checkpoints from this link : Extract the .tar.gz file and place each directory in the /logs directory. (We provide TSP20, TSP50 and TSP100 models.)

Installation

We ran our code on Ubuntu 16.04, using Python 3.6.7, PyTorch 0.4.1 and CUDA 9.0.

Note: This codebase was developed for a rather outdated version of PyTorch. Attempting to run the code with PyTorch 1.x may need further modifications, e.g. see this issue .

Step-by-step guide for local installation using a Terminal (Mac/Linux) or Git Bash (Windows) via Anaconda:

Running in Notebook/Visualization Mode

Launch Jupyter Lab and execute/modify main.ipynb cell-by-cell in Notebook Mode.

Set viz_mode = True in the first cell of main.ipynb to toggle Visualization Mode.

Running in Script Mode

Set notebook_mode = False and viz_mode = False in the first cell of main.ipynb . Then convert the notebook from .ipynb to .py and run the script (pass path of config file as arguement):

Splitting datasets into Training and Validation sets

For TSP10, TSP20 and TSP30 datasets, everything is good to go once you download and extract the files. For TSP50 and TSP100, the 1M training set needs to be split into 10K validation samples and 999K training samples. Use the split_train_val.py script to do so. For consistency, the script uses the first 10K samples in the 1M file as the validation set and the remaining 999K as the training set.

Generating new data

New TSP data can be generated using the Concorde solver .

• Optimal TSP Datasets generated with Concorde
• Paper on arXiv
• Follow-up workshop paper
• Python 54.7%
• Jupyter Notebook 45.3%