how many time travel paradoxes are there

[ November 30, 2022 ] The Night Sky This Month: December 2022 Night Sky
[ November 22, 2022 ] James Webb Telescope Turns Its Attention To The Kuiper Belt News & Events
[ November 1, 2022 ] The Night Sky This Month: November 2022 Night Sky
[ October 4, 2022 ] Are Wormholes Fact or Fiction? General Astronomy
[ October 1, 2022 ] The Night Sky This Month: October 2022 Night Sky

5 Bizarre Paradoxes Of Time Travel Explained

December 20, 2014 James Miller Astronomy Lists , Time Travel 58

There is nothing in Einstein’s theories of relativity to rule out time travel , although the very notion of traveling to the past violates one of the most fundamental premises of physics, that of causality. With the laws of cause and effect out the window, there naturally arises a number of inconsistencies associated with time travel, and listed here are some of those paradoxes which have given both scientists and time travel movie buffs alike more than a few sleepless nights over the years.

Types of Temporal Paradoxes

The time travel paradoxes that follow fall into two broad categories:

1) Closed Causal Loops , such as the Predestination Paradox and the Bootstrap Paradox, which involve a self-existing time loop in which cause and effect run in a repeating circle, but is also internally consistent with the timeline’s history.

2) Consistency Paradoxes , such as the Grandfather Paradox and other similar variants such as The Hitler paradox, and Polchinski’s Paradox, which generate a number of timeline inconsistencies related to the possibility of altering the past.

1: Predestination Paradox

A Predestination Paradox occurs when the actions of a person traveling back in time become part of past events, and may ultimately cause the event he is trying to prevent to take place. The result is a ‘temporal causality loop’ in which Event 1 in the past influences Event 2 in the future (time travel to the past) which then causes Event 1 to occur.

This circular loop of events ensures that history is not altered by the time traveler, and that any attempts to stop something from happening in the past will simply lead to the cause itself, instead of stopping it. Predestination paradoxes suggest that things are always destined to turn out the same way and that whatever has happened must happen.

Sound complicated? Imagine that your lover dies in a hit-and-run car accident, and you travel back in time to save her from her fate, only to find that on your way to the accident you are the one who accidentally runs her over. Your attempt to change the past has therefore resulted in a predestination paradox. One way of dealing with this type of paradox is to assume that the version of events you have experienced are already built into a self-consistent version of reality, and that by trying to alter the past you will only end up fulfilling your role in creating an event in history, not altering it.

– Cinema Treatment

In The Time Machine (2002) movie, for instance, Dr. Alexander Hartdegen witnesses his fiancee being killed by a mugger, leading him to build a time machine to travel back in time to save her from her fate. His subsequent attempts to save her fail, though, leading him to conclude that “I could come back a thousand times… and see her die a thousand ways.” After then traveling centuries into the future to see if a solution has been found to the temporal problem, Hartdegen is told by the Über-Morlock:

“You built your time machine because of Emma’s death. If she had lived, it would never have existed, so how could you use your machine to go back and save her? You are the inescapable result of your tragedy, just as I am the inescapable result of you .”

Movies : Examples of predestination paradoxes in the movies include 12 Monkeys (1995), TimeCrimes (2007), The Time Traveler’s Wife (2009), and Predestination (2014).
Books : An example of a predestination paradox in a book is Phoebe Fortune and the Pre-destination Paradox by M.S. Crook.

2: Bootstrap Paradox

A Bootstrap Paradox is a type of paradox in which an object, person, or piece of information sent back in time results in an infinite loop where the object has no discernible origin, and exists without ever being created. It is also known as an Ontological Paradox, as ontology is a branch of philosophy concerned with the nature of being or existence.

– Information : George Lucas traveling back in time and giving himself the scripts for the Star War movies which he then goes on to direct and gain great fame for would create a bootstrap paradox involving information, as the scripts have no true point of creation or origin.

– Person : A bootstrap paradox involving a person could be, say, a 20-year-old male time traveler who goes back 21 years, meets a woman, has an affair, and returns home three months later without knowing the woman was pregnant. Her child grows up to be the 20-year-old time traveler, who travels back 21 years through time, meets a woman, and so on. American science fiction writer Robert Heinlein wrote a strange short story involving a sexual paradox in his 1959 classic “All You Zombies.”

These ontological paradoxes imply that the future, present, and past are not defined, thus giving scientists an obvious problem on how to then pinpoint the “origin” of anything, a word customarily referring to the past, but now rendered meaningless. Further questions arise as to how the object/data was created, and by whom. Nevertheless, Einstein’s field equations allow for the possibility of closed time loops, with Kip Thorne the first theoretical physicist to recognize traversable wormholes and backward time travel as being theoretically possible under certain conditions.

Movies : Examples of bootstrap paradoxes in the movies include Somewhere in Time (1980), Bill and Ted’s Excellent Adventure (1989), the Terminator movies, and Time Lapse (2014). The Netflix series Dark (2017-19) also features a book called ‘A Journey Through Time’ which presents another classic example of a bootstrap paradox.
Books : Examples of bootstrap paradoxes in books include Michael Moorcock’s ‘Behold The Man’, Tim Powers’ The Anubis Gates, and Heinlein’s “By His Bootstraps”

3: Grandfather Paradox

The Grandfather Paradox concerns ‘self-inconsistent solutions’ to a timeline’s history caused by traveling back in time. For example, if you traveled to the past and killed your grandfather, you would never have been born and would not have been able to travel to the past – a paradox.

Let’s say you did decide to kill your grandfather because he created a dynasty that ruined the world. You figure if you knock him off before he meets your grandmother then the whole family line (including you) will vanish and the world will be a better place. According to theoretical physicists, the situation could play out as follows:

– Timeline protection hypothesis: You pop back in time, walk up to him, and point a revolver at his head. You pull the trigger but the gun fails to fire. Click! Click! Click! The bullets in the chamber have dents in the firing caps. You point the gun elsewhere and pull the trigger. Bang! Point it at your grandfather.. Click! Click! Click! So you try another method to kill him, but that only leads to scars that in later life he attributed to the world’s worst mugger. You can do many things as long as they’re not fatal until you are chased off by a policeman.

– Multiple universes hypothesis: You pop back in time, walk up to him, and point a revolver at his head. You pull the trigger and Boom! The deed is done. You return to the “present,” but you never existed here. Everything about you has been erased, including your family, friends, home, possessions, bank account, and history. You’ve entered a timeline where you never existed. Scientists entertain the possibility that you have now created an alternate timeline or entered a parallel universe.

Movies : Example of the Grandfather Paradox in movies include Back to the Future (1985), Back to the Future Part II (1989), and Back to the Future Part III (1990).
Books : Example of the Grandfather Paradox in books include Dr. Quantum in the Grandfather Paradox by Fred Alan Wolf , The Grandfather Paradox by Steven Burgauer, and Future Times Three (1944) by René Barjavel, the very first treatment of a grandfather paradox in a novel.

4: Let’s Kill Hitler Paradox

Similar to the Grandfather Paradox which paradoxically prevents your own birth, the Killing Hitler paradox erases your own reason for going back in time to kill him. Furthermore, while killing Grandpa might have a limited “butterfly effect,” killing Hitler would have far-reaching consequences for everyone in the world, even if only for the fact you studied him in school.

The paradox itself arises from the idea that if you were successful, then there would be no reason to time travel in the first place. If you killed Hitler then none of his actions would trickle down through history and cause you to want to make the attempt.

Movies/Shows : By far the best treatment for this notion occurred in a Twilight Zone episode called Cradle of Darkness which sums up the difficulties involved in trying to change history, with another being an episode of Dr Who called ‘Let’s Kill Hitler’.
Books : Examples of the Let’s Kill Hitler Paradox in books include How to Kill Hitler: A Guide For Time Travelers by Andrew Stanek, and the graphic novel I Killed Adolf Hitler by Jason.

5: Polchinski’s Paradox

American theoretical physicist Joseph Polchinski proposed a time paradox scenario in which a billiard ball enters a wormhole, and emerges out the other end in the past just in time to collide with its younger version and stop it from going into the wormhole in the first place.

Polchinski’s paradox is taken seriously by physicists, as there is nothing in Einstein’s General Relativity to rule out the possibility of time travel, closed time-like curves (CTCs), or tunnels through space-time. Furthermore, it has the advantage of being based upon the laws of motion, without having to refer to the indeterministic concept of free will, and so presents a better research method for scientists to think about the paradox. When Joseph Polchinski proposed the paradox, he had Novikov’s Self-Consistency Principle in mind, which basically states that while time travel is possible, time paradoxes are forbidden.

However, a number of solutions have been formulated to avoid the inconsistencies Polchinski suggested, which essentially involves the billiard ball delivering a blow that changes its younger version’s course, but not enough to stop it from entering the wormhole. This solution is related to the ‘timeline-protection hypothesis’ which states that a probability distortion would occur in order to prevent a paradox from happening. This also helps explain why if you tried to time travel and murder your grandfather, something will always happen to make that impossible, thus preserving a consistent version of history.

Books: Paradoxes of Time Travel by Ryan Wasserman is a wide-ranging exploration of time and time travel, including Polchinski’s Paradox.

Are Self-Fulfilling Prophecies Paradoxes?

A self-fulfilling prophecy is only a causality loop when the prophecy is truly known to happen and events in the future cause effects in the past, otherwise the phenomenon is not so much a paradox as a case of cause and effect. Say, for instance, an authority figure states that something is inevitable, proper, and true, convincing everyone through persuasive style. People, completely convinced through rhetoric, begin to behave as if the prediction were already true, and consequently bring it about through their actions. This might be seen best by an example where someone convincingly states:

“High-speed Magnetic Levitation Trains will dominate as the best form of transportation from the 21st Century onward.”

Jet travel, relying on diminishing fuel supplies, will be reserved for ocean crossing, and local flights will be a thing of the past. People now start planning on building networks of high-speed trains that run on electricity. Infrastructure gears up to supply the needed parts and the prediction becomes true not because it was truly inevitable (though it is a smart idea), but because people behaved as if it were true.

It even works on a smaller scale – the scale of individuals. The basic methodology for all those “self-help” books out in the world is that if you modify your thinking that you are successful (money, career, dating, etc.), then with the strengthening of that belief you start to behave like a successful person. People begin to notice and start to treat you like a successful person; it is a reinforcement/feedback loop and you actually become successful by behaving as if you were.

Are Time Paradoxes Inevitable?

The Butterfly Effect is a reference to Chaos Theory where seemingly trivial changes can have huge cascade reactions over long periods of time. Consequently, the Timeline corruption hypothesis states that time paradoxes are an unavoidable consequence of time travel, and even insignificant changes may be enough to alter history completely.

In one story, a paleontologist, with the help of a time travel device, travels back to the Jurassic Period to get photographs of Stegosaurus, Brachiosaurus, Ceratosaurus, and Allosaurus amongst other dinosaurs. He knows he can’t take samples so he just takes magnificent pictures from the fixed platform that is positioned precisely to not change anything about the environment. His assistant is about to pick a long blade of grass, but he stops him and explains how nothing must change because of their presence. They finish what they are doing and return to the present, but everything is gone. They reappear in a wild world with no humans and no signs that they ever existed. They fall to the floor of their platform, the only man-made thing in the whole world, and lament “Why? We didn’t change anything!” And there on the heel of the scientist’s shoe is a crushed butterfly.

The Butterfly Effect is also a movie, starring Ashton Kutcher as Evan Treborn and Amy Smart as Kayleigh Miller, where a troubled man has had blackouts during his youth, later explained by him traveling back into his own past and taking charge of his younger body briefly. The movie explores the issue of changing the timeline and how unintended consequences can propagate.

Scientists eager to avoid the paradoxes presented by time travel have come up with a number of ingenious ways in which to present a more consistent version of reality, some of which have been touched upon here, including:

The Solution: time travel is impossible because of the very paradox it creates.
Self-healing hypothesis: successfully altering events in the past will set off another set of events which will cause the present to remain the same.
The Multiverse or “many-worlds” hypothesis: an alternate parallel universe or timeline is created each time an event is altered in the past.
Erased timeline hypothesis : a person traveling to the past would exist in the new timeline, but have their own timeline erased.

a graphic of a tunnel in outer space with eight analog alarm clocks appearing to tumb;e through the tunnel

Is time travel even possible? An astrophysicist explains the science behind the science fiction

Assistant Professor of Astronomy and Astrophysics, University of Maryland, Baltimore County

Disclosure statement

Adi Foord does not work for, consult, own shares in or receive funding from any company or organisation that would benefit from this article, and has disclosed no relevant affiliations beyond their academic appointment.

University of Maryland, Baltimore County provides funding as a member of The Conversation US.

View all partners

Curious Kids is a series for children of all ages. If you have a question you’d like an expert to answer, send it to [email protected] .

Will it ever be possible for time travel to occur? – Alana C., age 12, Queens, New York

Have you ever dreamed of traveling through time, like characters do in science fiction movies? For centuries, the concept of time travel has captivated people’s imaginations. Time travel is the concept of moving between different points in time, just like you move between different places. In movies, you might have seen characters using special machines, magical devices or even hopping into a futuristic car to travel backward or forward in time.

But is this just a fun idea for movies, or could it really happen?

The question of whether time is reversible remains one of the biggest unresolved questions in science. If the universe follows the laws of thermodynamics , it may not be possible. The second law of thermodynamics states that things in the universe can either remain the same or become more disordered over time.

It’s a bit like saying you can’t unscramble eggs once they’ve been cooked. According to this law, the universe can never go back exactly to how it was before. Time can only go forward, like a one-way street.

Time is relative

However, physicist Albert Einstein’s theory of special relativity suggests that time passes at different rates for different people. Someone speeding along on a spaceship moving close to the speed of light – 671 million miles per hour! – will experience time slower than a person on Earth.

People have yet to build spaceships that can move at speeds anywhere near as fast as light, but astronauts who visit the International Space Station orbit around the Earth at speeds close to 17,500 mph. Astronaut Scott Kelly has spent 520 days at the International Space Station, and as a result has aged a little more slowly than his twin brother – and fellow astronaut – Mark Kelly. Scott used to be 6 minutes younger than his twin brother. Now, because Scott was traveling so much faster than Mark and for so many days, he is 6 minutes and 5 milliseconds younger .

Some scientists are exploring other ideas that could theoretically allow time travel. One concept involves wormholes , or hypothetical tunnels in space that could create shortcuts for journeys across the universe. If someone could build a wormhole and then figure out a way to move one end at close to the speed of light – like the hypothetical spaceship mentioned above – the moving end would age more slowly than the stationary end. Someone who entered the moving end and exited the wormhole through the stationary end would come out in their past.

However, wormholes remain theoretical: Scientists have yet to spot one. It also looks like it would be incredibly challenging to send humans through a wormhole space tunnel.

Paradoxes and failed dinner parties

There are also paradoxes associated with time travel. The famous “ grandfather paradox ” is a hypothetical problem that could arise if someone traveled back in time and accidentally prevented their grandparents from meeting. This would create a paradox where you were never born, which raises the question: How could you have traveled back in time in the first place? It’s a mind-boggling puzzle that adds to the mystery of time travel.

Famously, physicist Stephen Hawking tested the possibility of time travel by throwing a dinner party where invitations noting the date, time and coordinates were not sent out until after it had happened. His hope was that his invitation would be read by someone living in the future, who had capabilities to travel back in time. But no one showed up.

As he pointed out : “The best evidence we have that time travel is not possible, and never will be, is that we have not been invaded by hordes of tourists from the future.”

Telescopes are time machines

Interestingly, astrophysicists armed with powerful telescopes possess a unique form of time travel. As they peer into the vast expanse of the cosmos, they gaze into the past universe. Light from all galaxies and stars takes time to travel, and these beams of light carry information from the distant past. When astrophysicists observe a star or a galaxy through a telescope, they are not seeing it as it is in the present, but as it existed when the light began its journey to Earth millions to billions of years ago.

NASA’s newest space telescope, the James Webb Space Telescope , is peering at galaxies that were formed at the very beginning of the Big Bang, about 13.7 billion years ago.

While we aren’t likely to have time machines like the ones in movies anytime soon, scientists are actively researching and exploring new ideas. But for now, we’ll have to enjoy the idea of time travel in our favorite books, movies and dreams.

Hello, curious kids! Do you have a question you’d like an expert to answer? Ask an adult to send your question to [email protected] . Please tell us your name, age and the city where you live.

And since curiosity has no age limit – adults, let us know what you’re wondering, too. We won’t be able to answer every question, but we will do our best.

Time travel
Special Relativity
Thermodynamics
Stephen Hawking
Curious Kids
Curious Kids US
Time travel paradox

Deputy Social Media Producer

Research Fellow /Senior Research Fellow – Implementation Science

Associate Professor, Occupational Therapy

GRAINS RESEARCH AND DEVELOPMENT CORPORATION CHAIRPERSON

Faculty of Law - Academic Appointment Opportunities

How Time Travel Works

Share Content on Facebook
Share Content on LinkedIn
Share Content on Flipboard
Share Content on Reddit
Share Content via Email

Time Travel Paradoxes

As we mentioned before, the concept of traveling into the past becomes a bit murky the second causality rears its head. Cause comes before effect, at least in this universe, which manages to muck up even the best-laid time traveling plans.

For starters, if you traveled back in time 200 years, you'd emerge in a time before you were born. Think about that for a second. In the flow of time, the effect (you) would exist before the cause (your birth).

To better understand what we're dealing with here, consider the famous grandfather paradox . You're a time-traveling assassin, and your target just happens to be your own grandfather. So you pop through the nearest wormhole and walk up to a spry 18-year-old version of your father's father. You raise your laser blaster , but just what happens when you pull the trigger?

Think about it. You haven't been born yet. Neither has your father. If you kill your own grandfather in the past, he'll never have a son. That son will never have you, and you'll never happen to take that job as a time-traveling assassin. You wouldn't exist to pull the trigger, thus negating the entire string of events. We call this an inconsistent causal loop .

On the other hand, we have to consider the idea of a consistent causal loop . While equally thought-provoking, this theoretical model of time travel is paradox free. According to physicist Paul Davies, such a loop might play out like this: A math professor travels into the future and steals a groundbreaking math theorem. The professor then gives the theorem to a promising student. Then, that promising student grows up to be the very person from whom the professor stole the theorem to begin with.

Then there's the post-selected model of time travel, which involves distorted probability close to any paradoxical situation [source: Sanders]. What does this mean? Well, put yourself in the shoes of the time-traveling assassin again. This time travel model would make your grandfather virtually death proof. You can pull the trigger, but the laser will malfunction. Perhaps a bird will poop at just the right moment, but some quantum fluctuation will occur to prevent a paradoxical situation from taking place.

But then there's another possibility: The quantum theory that the future or past you travel into might just be a parallel universe . Think of it as a separate sandbox: You can build or destroy all the castles you want in it, but it doesn't affect your home sandbox in the slightest. So if the past you travel into exists in a separate timeline, killing your grandfather in cold blood is no big whoop. Of course, this might mean that every time jaunt would land you in a new parallel universe and you might never return to your original sandbox.

Confused yet? Welcome to the world of time travel.

Explore the links below for even more mind-blowing cosmology.

How Time Works
How Special Relativity Works
What is relativity?
Is Time Travel Possible?
How Black Holes Work
How would time travel affect life as we know it?

The Time-Travel Paradoxes

What happens if a time traveler kills his or her grandfather? What is a time loop? How do you stop a time machine from just appearing somewhere in space, millions of kilometers from home? And is there such a thing as free will?

Congratulations! You have a time machine! You can pop over to see the dinosaurs, be in London for the Beatles’ rooftop concert, hear Jesus deliver his Sermon on the Mount, save the books of the Library of Alexandria, or kill Hitler. Past and future are in your hands. All you have to do is step inside and press the red button.

Wait! Don’t do it!

Seriously, if you value your lives, if you want to protect the fabric of reality – run for the hills! Physics and logical paradoxes will be your undoing. From the grandfather paradox to laws of classic mechanics, we have prepared a comprehensive guide to the hazards of time travel. Beware the dangers that lie ahead.

The machine from H. G. Wells’ “The Time Machine”. Credit: Shutterstock.

The Grandfather Paradox

Want to change reality? First think carefully about your grandparents’ contribution to your lives.

The grandfather paradox basically describes the following situation: For some reason or another, you have decided to go back in time and kill your grandfather in his youth. Yeah, sure, of course you love him – but this is a scientific experiment; you don’t have a choice. So your grandmother will never give birth to your parent – and therefore you will never be born, which means that you cannot kill your grandfather. Oh boy! This is quite a contradiction!

The extended version of the paradox touches upon practically every single change that our hypothetical time traveler will make in the past. In a chaotic reality, there is no telling what the consequences of each step will be on the reality you came from. Just as a butterfly flapping its wings in the Amazon could cause a tornado in Texas, there is no way of predicting what one wrong move on your part might do to all of history, let alone a drastic move like killing someone.

There is a possible solution to this paradox – but it cancels out free will: Our time traveler can only do what has already been done. So don’t worry – everything you did in the past has already happened, so it’s impossible for you to kill grandpa, or create any sort of a contradiction in any other way. Another solution is that the time traveler's actions led to a splitting of the universe into two universes – one in which the time traveler was born, and the other in which he murdered his grandfather and was not born.

Information passage from the future to the past causes a similar paradox. Let’s say someone from the future who has my best interests in mind tries to warn me that a grand piano is about to fall on my head in the street, or that I have a type of cancer that is curable if it’s discovered early enough. Because of this warning, I could take steps to prevent the event – but then, there is no reason to send back the information from the future that saves my life. Another contradiction!

Marty finds himself in hot water with the grandfather paradox, from ‘Back to the Future’ 1985

Let’s now assume the information is different: A richer future me builds a time machine to let the late-90s me know that I should buy stock of a small company called “Google”, so that I can make a fortune. If I have free will, that means I can refuse. But future me knows I already did it. Do I have a choice but to do what I ask of myself?

The Time Loop

In the book All You Zombies by science fiction writer Robert A. Heinlein the Hero is sent back in time in order to impregnate a young woman who is later revealed to be him, following a sex change operation. The offspring of this coupling is the young man himself, who will meet himself at a younger age and take him back to the past to impregnate you know whom.

Confused? This is just one extreme example of a time loop – a situation where a past event is the cause of an event at another time and also the result of it. A simpler example could be a time traveler giving the young William Shakespeare a copy of the complete works of Shakespeare so that he can copy them. If that happens, then who is the genius author of Macbeth?

This phenomenon is also known as the Bootstrap Paradox , based on another story by Heinlein, who likened it to a person trying to pull himself up by his bootstraps (a phrase which, in turn, comes from the classic book The Surprising Adventures of Baron Munchausen). The word ‘paradox’ here is a bit misleading, since there is no contradiction in the loop – it exists in a sequence of events and feeds itself. The only contradiction is in the order of things that we are acquainted with, where cause leads to effect and nothing further, and there is meaning to the question “how did it all begin?”

Terminator 2 (1991). The shapeshifting android (Arnold Schwarzenegger) destroys himself in order to break the time loop in which his mere presence in the present enabled his production in the future

Time travelers – where have all they gone?

In 1950, over lunch physicist Enrico Fermi famously asked: “If there is intelligent extraterrestrial life in the Universe – then where are they?” indicating that we have never met aliens or came across evidence of their existence, such as radio signals which would be proof of a technological society. We could pose that same question about time travelers: “If time travel is possible, where are all the time travelers?”

The question, known as the Fermi Paradox, is an important one. After all, if it were possible to travel through time, would we not have bumped into a bunch of observers from the future at critical junctures in history? It is unlikely to assume that they all managed to perfectly disguise themselves, without making any errors in the design of the clothes they wore, their accents, their vocabulary, etc. Another option is that time travel is possible, but it is used with the utmost care and tight control, due to all the dangers we discuss here.

But where is everybody? A painting of the Italian physicist Enrico Fermi – Emilio Segrè Visual Archives SPL

On June 28, 2009, physicist Stephen Hawking carried out a scientific experiment which was meant to answer this question once and for all. He brought snacks, balloons and champagne and hosted a secret party for time travelers only – but sent out the invitations only on the next day. If no one showed up, he argued, that would be proof that time travel to the past is not possible. The invitees failed to arrive. “I sat and waited for a while, but nobody came,” he reported at the Seattle Science Festival in 2012.

Multiple time travelers also undermine the possibility of a fixed and consistent timeline, assuming that the past can indeed be changed. Imagine, for example, a nail-biting derby between the top clubs, Hapoel Jericho and Maccabi Jericho. Originally Maccabi won, so a Hapoel fan traveled back in time and managed to lead to his team’s victory. Maccabi fans would not give up and did the same. Soon, the whole stadium is filled with time travelers and paradoxes.

One way or round trip?

When considering travel, it is always continuous – from point A to point B, through all the points in between. Time travel should supposedly be the same: travelers get into their machine, push the button, and go from time A to time B, through all the times in between. But there’s a catch, if we are only travelling through time, then to the casual observer, the time machine continuously exists in the same space between the points in time. The result is that our journey is one-way and the time travelers will stay stuck in the future or the past because the machine itself will block the time-path back. And that is before we even start wondering how to even build this thing in the first place if it already exists in the place where we want to build it.

If that’s the case, then there’s no choice but to assume that there is some way to jump from time to time or place to place and materialize at the destination. How will our machine “know” to jump to an empty area, and to avoid materializing into a wall or a living creature unlucky enough to occupy that same spot? The passengers will undoubtedly need effective navigation and observation equipment to prevent unfortunate accidents at the point of entry.

While travelling from one point in time to another are passengers passing through all the moments in between? Good question! Photo: Shutterstock

Advanced time travel

In addition to the problems that time travel poses for anyone trying to keep the notion of cause and effect in order, time travelers may also face – or already have faced – other challenges from physics, even classical physics.

One issue you have to consider during time travel, and which science fiction writers usually prefer to ignore for convenience sake, is the question of arrival at the specified time destination and what would happen to us there.

It is usually assumed, with no good reason, that if someone is travelling through time, he or she will land in the same place, but at a different time – past or future. But this is where we hit a snag: the Earth rotates around the sun at a speed of 110,000 kph, and the Solar System itself is moving in its trajectory around the galaxy at a speed of 750,000 kph. If we time-travel for even a few seconds and stay in the same coordinates of space, we will probably find ourselves floating in outer space and perhaps even manage a quick glance around before we die. Our time machine will have to take into account this movement of the heavenly bodies and place us at exactly the right spot in space.

This alone may be resolved, since time travel, in any case, takes place between two points in the four-dimensional space-time continuum. According to the theory of general relativity, the theoretical foundation for time travel, space and time are a single physical entity, known as space-time. This entity can be bent and distorted – in fact gravity itself is an external manifestation of space-time distortion.

The Time Lord ,Doctor Who explains what “time” is exactly (Doctor Who, Season 3, Chapter 10: Blink).

Time travel would be possible if we could create a closed space-time loop, or if we could go from one point to another through a shortcut called a “Wormhole”. This would, in any case, not be just moving from one point in time to another, but would also include moving through space. Thus, from the outset, the journey is not only in time, but necessarily includes a destination point in space, which we will need to pre-program on our machine, of course .

In practice, the situation is more complicated – especially if we want to go into the distant past or distant future. The speed of the celestial bodies, and even the Earth’s shape and the structure of the continents, the seas, and mountains on the face of the Earth, change over the years. And because even a tiny deviation in our knowledge of the past can land us in the core of the Earth, in outer space or somewhere else that immediately reduces life expectancy to zero – time travel becomes a Russian roulette.

How to travel in time and stay alive

Let’s assume we coped with this problem and managed to get to the exact point in space-time that can sustain life. Careful – we’re not there yet; we still have to deal with momentum.

Momentum is a conserved quantity, which basically represents the potential of a body to continue moving at the speed and direction in which it is already travelling. If we were to jump out of a moving car (heaven forbid!), conservation of momentum is what would cause us to roll on the ground and probably get injured (in the best-case scenario). And so, if we leap in time – say, a month back – and land at the exact same point on Earth – we would discover, much to our dismay, that even if we started motionless in relation to the ground, now the ground underneath us is moving quickly at one angle or another towards us . Thus, even if we were lucky enough not to crash immediately on impact, we’re likely to hit some obstacle. And if by some miracle we were to survive, we would quickly find ourselves burning up in the atmosphere or gasping for air in space – because we have far exceeded the escape velocity from Earth.

We still have to deal with the issue of momentum in our time travels / Illustrative picture, Shutterstock

A possible solution to this problem is to plan our landing point ahead, so that the ground speed will be equal in size and direction to our exit speed, but this places many constraints on our journey. We could always leap into space, where there are hardly any moving objects to be bumped into, and only then land again at our point of destination on Earth.

Having said all that, this problem arises chiefly when we assume that time hopping is immediate – that we disappear from one point in time and immediately appear in another, without losing mass, energy, or momentum. But since a “realistic” journey in time is not instantaneous, rather it involves travelling along space-time, it is no different from other types of journeys. This being the case, we can hope that we could adjust our speed to the desired value and direction prior to landing, just like a spacecraft slowing down before landing on a planet.

We should also keep in mind that thankfully, we will have access to a powerful technology that would enable us to cope with such problems: Time-travel technology itself. For example, we might decide to send thousands of tiny probes ahead of us, each to a slightly different point in space-time. Some of them, maybe even most, will be destroyed for one of the reasons already mentioned. The others will wait patiently until the present and then feed their programmed coordinates into the time machine. Thus by definition, the destination entered will be safe for us, except, perhaps for the annoying probe shower hitting the travellers. For the travellers themselves, the entire process will be immediate.

Time Travelling Grammar

Finally, we come to the question: How do you actually talk about time travel? The three tenses – past, present, and future – are insufficient to discuss a future event that happened some time in the past with someone who is in the present, which is another’s past and yet another’s future. And what is the correct grammatical tense to use when we talk about an alternative future that would have been created after we killed our grandfather? Or how do we express the future-past tense (or past-future, or past-future-past?), when we get stuck in a time loop where what will happen leads to what had already taken place, and so on? And of course the biggest question that Hebrew editors and translators have faced for years – is there really such a thing as present continuous?

It’s complicated.

Arguing about tenses and a time machine, The Big Bang Theory, Season 8, Episode 5, 2014

In his book, The Restaurant at the End of the Universe, science fiction writer Douglas Adams suggests to his readers to consult (by Dr. Dan Streetmentioner) Time Traveler's Handbook of 1001 Tense Formations (by Dr. Dan Streetmentioner) to find the answers to these questions. That’s all very well, but, Adams tells us, “most readers get as far as the Future Semi-Conditionally Modified Subinverted Plagal Past Subjunctive Intentional before giving up; and in fact in later editions of the book all pages beyond this point have been left blank to save on printing costs.”

If, despite all of the above, you’re still intent on travelling back to Mount Sinai or the Apollo 11 moon landing – let us then wish you bon voyage, and please give our regards to Neil Armstrong!

Table of Contents
Random Entry
Chronological
Editorial Information
About the SEP
Editorial Board
How to Cite the SEP
Special Characters
Advanced Tools
Support the SEP
PDFs for SEP Friends
Make a Donation
SEPIA for Libraries
Entry Contents

Bibliography

Academic tools.

Friends PDF Preview
Author and Citation Info
Back to Top

Time Travel and Modern Physics

Time travel has been a staple of science fiction. With the advent of general relativity it has been entertained by serious physicists. But, especially in the philosophy literature, there have been arguments that time travel is inherently paradoxical. The most famous paradox is the grandfather paradox: you travel back in time and kill your grandfather, thereby preventing your own existence. To avoid inconsistency some circumstance will have to occur which makes you fail in this attempt to kill your grandfather. Doesn’t this require some implausible constraint on otherwise unrelated circumstances? We examine such worries in the context of modern physics.

1. Paradoxes Lost?

2. topology and constraints, 3. the general possibility of time travel in general relativity, 4. two toy models, 5. slightly more realistic models of time travel, 6. the possibility of time travel redux, 7. even if there are constraints, so what, 8. computational models, 9. quantum mechanics to the rescue, 10. conclusions, other internet resources, related entries.

Supplement: Remarks and Limitations on the Toy Models

Modern physics strips away many aspects of the manifest image of time. Time as it appears in the equations of classical mechanics has no need for a distinguished present moment, for example. Relativity theory leads to even sharper contrasts. It replaces absolute simultaneity, according to which it is possible to unambiguously determine the time order of distant events, with relative simultaneity: extending an “instant of time” throughout space is not unique, but depends on the state of motion of an observer. More dramatically, in general relativity the mathematical properties of time (or better, of spacetime)—its topology and geometry—depend upon how matter is arranged rather than being fixed once and for all. So physics can be, and indeed has to be, formulated without treating time as a universal, fixed background structure. Since general relativity represents gravity through spacetime geometry, the allowed geometries must be as varied as the ways in which matter can be arranged. Alongside geometrical models used to describe the solar system, black holes, and much else, the scope of variation extends to include some exotic structures unlike anything astrophysicists have observed. In particular, there are spacetime geometries with curves that loop back on themselves: closed timelike curves (CTCs), which describe the possible trajectory of an observer who returns exactly back to their earlier state—without any funny business, such as going faster than the speed of light. These geometries satisfy the relevant physical laws, the equations of general relativity, and in that sense time travel is physically possible.

Yet circular time generates paradoxes, familiar from science fiction stories featuring time travel: [ 1 ]

Consistency: Kurt plans to murder his own grandfather Adolph, by traveling along a CTC to an appropriate moment in the past. He is an able marksman, and waits until he has a clear shot at grandpa. Normally he would not miss. Yet if he succeeds, there is no way that he will then exist to plan and carry out the mission. Kurt pulls the trigger: what can happen?
Underdetermination: Suppose that Kurt first travels back in order to give his earlier self a copy of How to Build a Time Machine. This is the same book that allows him to build a time machine, which he then carries with him on his journey to the past. Who wrote the book?
Easy Knowledge: A fan of classical music enhances their computer with a circuit that exploits a CTC. This machine efficiently solves problems at a higher level of computational complexity than conventional computers, leading (among other things) to finding the smallest circuits that can generate Bach’s oeuvre—and to compose new pieces in the same style. Such easy knowledge is at odds with our understanding of our epistemic predicament. (This third paradox has not drawn as much attention.)

The first two paradoxes were once routinely taken to show that solutions with CTCs should be rejected—with charges varying from violating logic, to being “physically unreasonable”, to undermining the notion of free will. Closer analysis of the paradoxes has largely reversed this consensus. Physicists have discovered many solutions with CTCs and have explored their properties in pursuing foundational questions, such as whether physics is compatible with the idea of objective temporal passage (starting with Gödel 1949). Philosophers have also used time travel scenarios to probe questions about, among other things, causation, modality, free will, and identity (see, e.g., Earman 1972 and Lewis’s seminal 1976 paper).

We begin below with Consistency , turning to the other paradoxes in later sections. A standard, stone-walling response is to insist that the past cannot be changed, as a matter of logic, even by a time traveler (e.g., Gödel 1949, Clarke 1977, Horwich 1987). Adolph cannot both die and survive, as a matter of logic, so any scheme to alter the past must fail. In many of the best time travel fictions, the actions of a time traveler are constrained in novel and unexpected ways. Attempts to change the past fail, and they fail, often tragically, in just such a way that they set the stage for the time traveler’s self-defeating journey. The first question is whether there is an analog of the consistent story when it comes to physics in the presence of CTCs. As we will see, there is a remarkable general argument establishing the existence of consistent solutions. Yet a second question persists: why can’t time-traveling Kurt kill his own grandfather? Doesn’t the necessity of failures to change the past put unusual and unexpected constraints on time travelers, or objects that move along CTCs? The same argument shows that there are in fact no constraints imposed by the existence of CTCs, in some cases. After discussing this line of argument, we will turn to the palatability and further implications of such constraints if they are required, and then turn to the implications of quantum mechanics.

Wheeler and Feynman (1949) were the first to claim that the fact that nature is continuous could be used to argue that causal influences from later events to earlier events, as are made possible by time travel, will not lead to paradox without the need for any constraints. Maudlin (1990) showed how to make their argument precise and more general, and argued that nonetheless it was not completely general.

Imagine the following set-up. We start off having a camera with a black and white film ready to take a picture of whatever comes out of the time machine. An object, in fact a developed film, comes out of the time machine. We photograph it, and develop the film. The developed film is subsequently put in the time machine, and set to come out of the time machine at the time the picture is taken. This surely will create a paradox: the developed film will have the opposite distribution of black, white, and shades of gray, from the object that comes out of the time machine. For developed black and white films (i.e., negatives) have the opposite shades of gray from the objects they are pictures of. But since the object that comes out of the time machine is the developed film itself it we surely have a paradox.

However, it does not take much thought to realize that there is no paradox here. What will happen is that a uniformly gray picture will emerge, which produces a developed film that has exactly the same uniform shade of gray. No matter what the sensitivity of the film is, as long as the dependence of the brightness of the developed film depends in a continuous manner on the brightness of the object being photographed, there will be a shade of gray that, when photographed, will produce exactly the same shade of gray on the developed film. This is the essence of Wheeler and Feynman’s idea. Let us first be a bit more precise and then a bit more general.

For simplicity let us suppose that the film is always a uniform shade of gray (i.e., at any time the shade of gray does not vary by location on the film). The possible shades of gray of the film can then be represented by the (real) numbers from 0, representing pure black, to 1, representing pure white.

Let us now distinguish various stages in the chronological order of the life of the film. In stage $S_1$ the film is young; it has just been placed in the camera and is ready to be exposed. It is then exposed to the object that comes out of the time machine. (That object in fact is a later stage of the film itself). By the time we come to stage $S_2$ of the life of the film, it has been developed and is about to enter the time machine. Stage $S_3$ occurs just after it exits the time machine and just before it is photographed. Stage $S_4$ occurs after it has been photographed and before it starts fading away. Let us assume that the film starts out in stage $S_1$ in some uniform shade of gray, and that the only significant change in the shade of gray of the film occurs between stages $S_1$ and $S_2$. During that period it acquires a shade of gray that depends on the shade of gray of the object that was photographed. In other words, the shade of gray that the film acquires at stage $S_2$ depends on the shade of gray it has at stage $S_3$. The influence of the shade of gray of the film at stage $S_3$, on the shade of gray of the film at stage $S_2$, can be represented as a mapping, or function, from the real numbers between 0 and 1 (inclusive), to the real numbers between 0 and 1 (inclusive). Let us suppose that the process of photography is such that if one imagines varying the shade of gray of an object in a smooth, continuous manner then the shade of gray of the developed picture of that object will also vary in a smooth, continuous manner. This implies that the function in question will be a continuous function. Now any continuous function from the real numbers between 0 and 1 (inclusive) to the real numbers between 0 and 1 (inclusive) must map at least one number to itself. One can quickly convince oneself of this by graphing such functions. For one will quickly see that any continuous function $f$ from $[0,1]$ to $[0,1]$ must intersect the line $x=y$ somewhere, and thus there must be at least one point $x$ such that $f(x)=x$. Such points are called fixed points of the function. Now let us think about what such a fixed point represents. It represents a shade of gray such that, when photographed, it will produce a developed film with exactly that same shade of gray. The existence of such a fixed point implies a solution to the apparent paradox.

Let us now be more general and allow color photography. One can represent each possible color of an object (of uniform color) by the proportions of blue, green and red that make up that color. (This is why television screens can produce all possible colors.) Thus one can represent all possible colors of an object by three points on three orthogonal lines $x, y$ and $z$, that is to say, by a point in a three-dimensional cube. This cube is also known as the “Cartesian product” of the three line segments. Now, one can also show that any continuous map from such a cube to itself must have at least one fixed point. So color photography can not be used to create time travel paradoxes either!

Even more generally, consider some system $P$ which, as in the above example, has the following life. It starts in some state $S_1$, it interacts with an object that comes out of a time machine (which happens to be its older self), it travels back in time, it interacts with some object (which happens to be its younger self), and finally it grows old and dies. Let us assume that the set of possible states of $P$ can be represented by a Cartesian product of $n$ closed intervals of the reals, i.e., let us assume that the topology of the state-space of $P$ is isomorphic to a finite Cartesian product of closed intervals of the reals. Let us further assume that the development of $P$ in time, and the dependence of that development on the state of objects that it interacts with, is continuous. Then, by a well-known fixed point theorem in topology (see, e.g., Hocking & Young 1961: 273), no matter what the nature of the interaction is, and no matter what the initial state of the object is, there will be at least one state $S_3$ of the older system (as it emerges from the time travel machine) that will influence the initial state $S_1$ of the younger system (when it encounters the older system) so that, as the younger system becomes older, it develops exactly into state $S_3$. Thus without imposing any constraints on the initial state $S_1$ of the system $P$, we have shown that there will always be perfectly ordinary, non-paradoxical, solutions, in which everything that happens, happens according to the usual laws of development. Of course, there is looped causation, hence presumably also looped explanation, but what do you expect if there is looped time?

Unfortunately, for the fan of time travel, a little reflection suggests that there are systems for which the needed fixed point theorem does not hold. Imagine, for instance, that we have a dial that can only rotate in a plane. We are going to put the dial in the time machine. Indeed we have decided that if we see the later stage of the dial come out of the time machine set at angle $x$, then we will set the dial to $x+90$, and throw it into the time machine. Now it seems we have a paradox, since the mapping that consists of a rotation of all points in a circular state-space by 90 degrees does not have a fixed point. And why wouldn’t some state-spaces have the topology of a circle?

However, we have so far not used another continuity assumption which is also a reasonable assumption. So far we have only made the following demand: the state the dial is in at stage $S_2$ must be a continuous function of the state of the dial at stage $S_3$. But, the state of the dial at stage $S_2$ is arrived at by taking the state of the dial at stage $S_1$, and rotating it over some angle. It is not merely the case that the effect of the interaction, namely the state of the dial at stage $S_2$, should be a continuous function of the cause, namely the state of the dial at stage $S_3$. It is additionally the case that path taken to get there, the way the dial is rotated between stages $S_1$ and $S_2$ must be a continuous function of the state at stage $S_3$. And, rather surprisingly, it turns out that this can not be done. Let us illustrate what the problem is before going to a more general demonstration that there must be a fixed point solution in the dial case.

Forget time travel for the moment. Suppose that you and I each have a watch with a single dial neither of which is running. My watch is set at 12. You are going to announce what your watch is set at. My task is going to be to adjust my watch to yours no matter what announcement you make. And my actions should have a continuous (single valued) dependence on the time that you announce. Surprisingly, this is not possible! For instance, suppose that if you announce “12”, then I achieve that setting on my watch by doing nothing. Now imagine slowly and continuously increasing the announced times, starting at 12. By continuity, I must achieve each of those settings by rotating my dial to the right. If at some point I switch and achieve the announced goal by a rotation of my dial to the left, I will have introduced a discontinuity in my actions, a discontinuity in the actions that I take as a function of the announced angle. So I will be forced, by continuity, to achieve every announcement by rotating the dial to the right. But, this rotation to the right will have to be abruptly discontinued as the announcements grow larger and I eventually approach 12 again, since I achieved 12 by not rotating the dial at all. So, there will be a discontinuity at 12 at the latest. In general, continuity of my actions as a function of announced times can not be maintained throughout if I am to be able to replicate all possible settings. Another way to see the problem is that one can similarly reason that, as one starts with 12, and imagines continuously making the announced times earlier, one will be forced, by continuity, to achieve the announced times by rotating the dial to the left. But the conclusions drawn from the assumption of continuous increases and the assumption of continuous decreases are inconsistent. So we have an inconsistency following from the assumption of continuity and the assumption that I always manage to set my watch to your watch. So, a dial developing according to a continuous dynamics from a given initial state, can not be set up so as to react to a second dial, with which it interacts, in such a way that it is guaranteed to always end up set at the same angle as the second dial. Similarly, it can not be set up so that it is guaranteed to always end up set at 90 degrees to the setting of the second dial. All of this has nothing to do with time travel. However, the impossibility of such set ups is what prevents us from enacting the rotation by 90 degrees that would create paradox in the time travel setting.

Let us now give the positive result that with such dials there will always be fixed point solutions, as long as the dynamics is continuous. Let us call the state of the dial before it interacts with its older self the initial state of the dial. And let us call the state of the dial after it emerges from the time machine the final state of the dial. There is also an intermediate state of the dial, after it interacts with its older self and before it is put into the time machine. We can represent the initial or intermediate states of the dial, before it goes into the time machine, as an angle $x$ in the horizontal plane and the final state of the dial, after it comes out of the time machine, as an angle $y$ in the vertical plane. All possible $\langle x,y\rangle$ pairs can thus be visualized as a torus with each $x$ value picking out a vertical circular cross-section and each $y$ picking out a point on that cross-section. See figure 1 .

Figure 1 [An extended description of figure 1 is in the supplement.]

Suppose that the dial starts at angle $i$ which picks out vertical circle $I$ on the torus. The initial angle $i$ that the dial is at before it encounters its older self, and the set of all possible final angles that the dial can have when it emerges from the time machine is represented by the circle $I$ on the torus (see figure 1 ). Given any possible angle of the emerging dial, the dial initially at angle $i$ will develop to some other angle. One can picture this development by rotating each point on $I$ in the horizontal direction by the relevant amount. Since the rotation has to depend continuously on the angle of the emerging dial, circle $I$ during this development will deform into some loop $L$ on the torus. Loop $L$ thus represents all possible intermediate angles $x$ that the dial is at when it is thrown into the time machine, given that it started at angle $i$ and then encountered a dial (its older self) which was at angle $y$ when it emerged from the time machine. We therefore have consistency if $x=y$ for some $x$ and $y$ on loop $L$. Now, let loop $C$ be the loop which consists of all the points on the torus for which $x=y$. Ring $I$ intersects $C$ at point $\langle i,i\rangle$. Obviously any continuous deformation of $I$ must still intersect $C$ somewhere. So $L$ must intersect $C$ somewhere, say at $\langle j,j\rangle$. But that means that no matter how the development of the dial starting at $I$ depends on the angle of the emerging dial, there will be some angle for the emerging dial such that the dial will develop exactly into that angle (by the time it enters the time machine) under the influence of that emerging dial. This is so no matter what angle one starts with, and no matter how the development depends on the angle of the emerging dial. Thus even for a circular state-space there are no constraints needed other than continuity.

Unfortunately there are state-spaces that escape even this argument. Consider for instance a pointer that can be set to all values between 0 and 1, where 0 and 1 are not possible values. That is, suppose that we have a state-space that is isomorphic to an open set of real numbers. Now suppose that we have a machine that sets the pointer to half the value that the pointer is set at when it emerges from the time machine.

Figure 2 [An extended description of figure 2 is in the supplement.]

Suppose the pointer starts at value $I$. As before we can represent the combination of this initial position and all possible final positions by the line $I$. Under the influence of the pointer coming out of the time machine the pointer value will develop to a value that equals half the value of the final value that it encountered. We can represent this development as the continuous deformation of line $I$ into line $L$, which is indicated by the arrows in figure 2 . This development is fully continuous. Points $\langle x,y\rangle$ on line $I$ represent the initial position $x=I$ of the (young) pointer, and the position $y$ of the older pointer as it emerges from the time machine. Points $\langle x,y\rangle$ on line $L$ represent the position $x$ that the younger pointer should develop into, given that it encountered the older pointer emerging from the time machine set at position $y$. Since the pointer is designed to develop to half the value of the pointer that it encounters, the line $L$ corresponds to $x=1/2 y$. We have consistency if there is some point such that it develops into that point, if it encounters that point. Thus, we have consistency if there is some point $\langle x,y\rangle$ on line $L$ such that $x=y$. However, there is no such point: lines $L$ and $C$ do not intersect. Thus there is no consistent solution, despite the fact that the dynamics is fully continuous.

Of course if 0 were a possible value, $L$ and $C$ would intersect at 0. This is surprising and strange: adding one point to the set of possible values of a quantity here makes the difference between paradox and peace. One might be tempted to just add the extra point to the state-space in order to avoid problems. After all, one might say, surely no measurements could ever tell us whether the set of possible values includes that exact point or not. Unfortunately there can be good theoretical reasons for supposing that some quantity has a state-space that is open: the set of all possible speeds of massive objects in special relativity surely is an open set, since it includes all speeds up to, but not including, the speed of light. Quantities that have possible values that are not bounded also lead to counter examples to the presented fixed point argument. And it is not obvious to us why one should exclude such possibilities. So the argument that no constraints are needed is not fully general.

An interesting question of course is: exactly for which state-spaces must there be such fixed points? The arguments above depend on a well-known fixed point theorem (due to Schauder) that guarantees the existence of a fixed point for compact, convex state spaces. We do not know what subsequent extensions of this result imply regarding fixed points for a wider variety of systems, or whether there are other general results along these lines. (See Kutach 2003 for more on this issue.)

A further interesting question is whether this line of argument is sufficient to resolve Consistency (see also Dowe 2007). When they apply, these results establish the existence of a solution, such as the shade of uniform gray in the first example. But physicists routinely demand more than merely the existence of a solution, namely that solutions to the equations are stable—such that “small” changes of the initial state lead to “small” changes of the resulting trajectory. (Clarifying the two senses of “small” in this statement requires further work, specifying the relevant topology.) Stability in this sense underwrites the possibility of applying equations to real systems given our inability to fix initial states with indefinite precision. (See Fletcher 2020 for further discussion.) The fixed point theorems guarantee that for an initial state $S_1$ there is a solution, but this solution may not be “close” to the solution for a nearby initial state, $S'$. We are not aware of any proofs that the solutions guaranteed to exist by the fixed point theorems are also stable in this sense.

Time travel has recently been discussed quite extensively in the context of general relativity. General relativity places few constraints on the global structure of space and time. This flexibility leads to a possibility first described in print by Hermann Weyl:

Every world-point is the origin of the double-cone of the active future and the passive past [i.e., the two lobes of the light cone]. Whereas in the special theory of relativity these two portions are separated by an intervening region, it is certainly possible in the present case [i.e., general relativity] for the cone of the active future to overlap with that of the passive past; so that, in principle, it is possible to experience events now that will in part be an effect of my future resolves and actions. Moreover, it is not impossible for a world-line (in particular, that of my body), although it has a timelike direction at every point, to return to the neighborhood of a point which it has already once passed through. (Weyl 1918/1920 [1952: 274])

A time-like curve is simply a space-time trajectory such that the speed of light is never equaled or exceeded along this trajectory. Time-like curves represent possible trajectories of ordinary objects. In general relativity a curve that is everywhere timelike locally can nonetheless loop back on itself, forming a CTC. Weyl makes the point vividly in terms of the light cones: along such a curve, the future lobe of the light cone (the “active future”) intersects the past lobe of the light cone (the “passive past”). Traveling along such a curve one would never exceed the speed of light, and yet after a certain amount of (proper) time one would return to a point in space-time that one previously visited. Or, by staying close to such a CTC, one could come arbitrarily close to a point in space-time that one previously visited. General relativity, in a straightforward sense, allows time travel: there appear to be many space-times compatible with the fundamental equations of general relativity in which there are CTC’s. Space-time, for instance, could have a Minkowski metric everywhere, and yet have CTC’s everywhere by having the temporal dimension (topologically) rolled up as a circle. Or, one can have wormhole connections between different parts of space-time which allow one to enter “mouth $A$” of such a wormhole connection, travel through the wormhole, exit the wormhole at “mouth $B$” and re-enter “mouth $A$” again. CTCs can even arise when the spacetime is topologically $\mathbb{R}^4$, due to the “tilting” of light cones produced by rotating matter (as in Gödel 1949’s spacetime).

General relativity thus appears to provide ample opportunity for time travel. Note that just because there are CTC’s in a space-time, this does not mean that one can get from any point in the space-time to any other point by following some future directed timelike curve—there may be insurmountable practical obstacles. In Gödel’s spacetime, it is the case that there are CTCs passing through every point in the spacetime. Yet these CTCs are not geodesics, so traversing them requires acceleration. Calculations of the minimal fuel required to travel along the appropriate curve should discourage any would-be time travelers (Malament 1984, 1985; Manchak 2011). But more generally CTCs may be confined to smaller regions; some parts of space-time can have CTC’s while other parts do not. Let us call the part of a space-time that has CTC’s the “time travel region” of that space-time, while calling the rest of that space-time the “normal region”. More precisely, the “time travel region” consists of all the space-time points $p$ such that there exists a (non-zero length) timelike curve that starts at $p$ and returns to $p$. Now let us turn to examining space-times with CTC’s a bit more closely for potential problems.

In order to get a feeling for the sorts of implications that closed timelike curves can have, it may be useful to consider two simple models. In space-times with closed timelike curves the traditional initial value problem cannot be framed in the usual way. For it presupposes the existence of Cauchy surfaces, and if there are CTCs then no Cauchy surface exists. (A Cauchy surface is a spacelike surface such that every inextendable timelike curve crosses it exactly once. One normally specifies initial conditions by giving the conditions on such a surface.) Nonetheless, if the topological complexities of the manifold are appropriately localized, we can come quite close. Let us call an edgeless spacelike surface $S$ a quasi-Cauchy surface if it divides the rest of the manifold into two parts such that

every point in the manifold can be connected by a timelike curve to $S$, and
any timelike curve which connects a point in one region to a point in the other region intersects $S$ exactly once.

It is obvious that a quasi-Cauchy surface must entirely inhabit the normal region of the space-time; if any point $p$ of $S$ is in the time travel region, then any timelike curve which intersects $p$ can be extended to a timelike curve which intersects $S$ near $p$ again. In extreme cases of time travel, a model may have no normal region at all (e.g., Minkowski space-time rolled up like a cylinder in a time-like direction), in which case our usual notions of temporal precedence will not apply. But temporal anomalies like wormholes (and time machines) can be sufficiently localized to permit the existence of quasi-Cauchy surfaces.

Given a timelike orientation, a quasi-Cauchy surface unproblematically divides the manifold into its past (i.e., all points that can be reached by past-directed timelike curves from $S)$ and its future (ditto mutatis mutandis ). If the whole past of $S$ is in the normal region of the manifold, then $S$ is a partial Cauchy surface : every inextendable timelike curve which exists to the past of $S$ intersects $S$ exactly once, but (if there is time travel in the future) not every inextendable timelike curve which exists to the future of $S$ intersects $S$. Now we can ask a particularly clear question: consider a manifold which contains a time travel region, but also has a partial Cauchy surface $S$, such that all of the temporal funny business is to the future of $S$. If all you could see were $S$ and its past, you would not know that the space-time had any time travel at all. The question is: are there any constraints on the sort of data which can be put on $S$ and continued to a global solution of the dynamics which are different from the constraints (if any) on the data which can be put on a Cauchy surface in a simply connected manifold and continued to a global solution? If there is time travel to our future, might we we able to tell this now, because of some implied oddity in the arrangement of present things?

It is not at all surprising that there might be constraints on the data which can be put on a locally space-like surface which passes through the time travel region: after all, we never think we can freely specify what happens on a space-like surface and on another such surface to its future, but in this case the surface at issue lies to its own future. But if there were particular constraints for data on a partial Cauchy surface then we would apparently need to have to rule out some sorts of otherwise acceptable states on $S$ if there is to be time travel to the future of $S$. We then might be able to establish that there will be no time travel in the future by simple inspection of the present state of the universe. As we will see, there is reason to suspect that such constraints on the partial Cauchy surface are non-generic. But we are getting ahead of ourselves: first let’s consider the effect of time travel on a very simple dynamics.

The simplest possible example is the Newtonian theory of perfectly elastic collisions among equally massive particles in one spatial dimension. The space-time is two-dimensional, so we can represent it initially as the Euclidean plane, and the dynamics is completely specified by two conditions. When particles are traveling freely, their world lines are straight lines in the space-time, and when two particles collide, they exchange momenta, so the collision looks like an “$X$” in space-time, with each particle changing its momentum at the impact. [ 2 ] The dynamics is purely local, in that one can check that a set of world-lines constitutes a model of the dynamics by checking that the dynamics is obeyed in every arbitrarily small region. It is also trivial to generate solutions from arbitrary initial data if there are no CTCs: given the initial positions and momenta of a set of particles, one simply draws a straight line from each particle in the appropriate direction and continues it indefinitely. Once all the lines are drawn, the worldline of each particle can be traced from collision to collision. The boundary value problem for this dynamics is obviously well-posed: any set of data at an instant yields a unique global solution, constructed by the method sketched above.

What happens if we change the topology of the space-time by hand to produce CTCs? The simplest way to do this is depicted in figure 3 : we cut and paste the space-time so it is no longer simply connected by identifying the line $L-$ with the line $L+$. Particles “going in” to $L+$ from below “emerge” from $L-$ , and particles “going in” to $L-$ from below “emerge” from $L+$.

Figure 3: Inserting CTCs by Cut and Paste. [An extended description of figure 3 is in the supplement.]

How is the boundary-value problem changed by this alteration in the space-time? Before the cut and paste, we can put arbitrary data on the simultaneity slice $S$ and continue it to a unique solution. After the change in topology, $S$ is no longer a Cauchy surface, since a CTC will never intersect it, but it is a partial Cauchy surface. So we can ask two questions. First, can arbitrary data on $S$ always be continued to a global solution? Second, is that solution unique? If the answer to the first question is $no$, then we have a backward-temporal constraint: the existence of the region with CTCs places constraints on what can happen on $S$ even though that region lies completely to the future of $S$. If the answer to the second question is $no$, then we have an odd sort of indeterminism, analogous to the unwritten book: the complete physical state on $S$ does not determine the physical state in the future, even though the local dynamics is perfectly deterministic and even though there is no other past edge to the space-time region in $S$’s future (i.e., there is nowhere else for boundary values to come from which could influence the state of the region).

In this case the answer to the first question is yes and to the second is no : there are no constraints on the data which can be put on $S$, but those data are always consistent with an infinitude of different global solutions. The easy way to see that there always is a solution is to construct the minimal solution in the following way. Start drawing straight lines from $S$ as required by the initial data. If a line hits $L-$ from the bottom, just continue it coming out of the top of $L+$ in the appropriate place, and if a line hits $L+$ from the bottom, continue it emerging from $L-$ at the appropriate place. Figure 4 represents the minimal solution for a single particle which enters the time-travel region from the left:

Figure 4: The Minimal Solution. [An extended description of figure 4 is in the supplement.]

The particle “travels back in time” three times. It is obvious that this minimal solution is a global solution, since the particle always travels inertially.

But the same initial state on $S$ is also consistent with other global solutions. The new requirement imposed by the topology is just that the data going into $L+$ from the bottom match the data coming out of $L-$ from the top, and the data going into $L-$ from the bottom match the data coming out of $L+$ from the top. So we can add any number of vertical lines connecting $L-$ and $L+$ to a solution and still have a solution. For example, adding a few such lines to the minimal solution yields:

Figure 5: A Non-Minimal Solution. [An extended description of figure 5 is in the supplement.]

The particle now collides with itself twice: first before it reaches $L+$ for the first time, and again shortly before it exits the CTC region. From the particle’s point of view, it is traveling to the right at a constant speed until it hits an older version of itself and comes to rest. It remains at rest until it is hit from the right by a younger version of itself, and then continues moving off, and the same process repeats later. It is clear that this is a global model of the dynamics, and that any number of distinct models could be generating by varying the number and placement of vertical lines.

Knowing the data on $S$, then, gives us only incomplete information about how things will go for the particle. We know that the particle will enter the CTC region, and will reach $L+$, we know that it will be the only particle in the universe, we know exactly where and with what speed it will exit the CTC region. But we cannot determine how many collisions the particle will undergo (if any), nor how long (in proper time) it will stay in the CTC region. If the particle were a clock, we could not predict what time it would indicate when exiting the region. Furthermore, the dynamics gives us no handle on what to think of the various possibilities: there are no probabilities assigned to the various distinct possible outcomes.

Changing the topology has changed the mathematics of the situation in two ways, which tend to pull in opposite directions. On the one hand, $S$ is no longer a Cauchy surface, so it is perhaps not surprising that data on $S$ do not suffice to fix a unique global solution. But on the other hand, there is an added constraint: data “coming out” of $L-$ must exactly match data “going in” to $L+$, even though what comes out of $L-$ helps to determine what goes into $L+$. This added consistency constraint tends to cut down on solutions, although in this case the additional constraint is more than outweighed by the freedom to consider various sorts of data on ${L+}/{L-}$.

The fact that the extra freedom outweighs the extra constraint also points up one unexpected way that the supposed paradoxes of time travel may be overcome. Let’s try to set up a paradoxical situation using the little closed time loop above. If we send a single particle into the loop from the left and do nothing else, we know exactly where it will exit the right side of the time travel region. Now suppose we station someone at the other side of the region with the following charge: if the particle should come out on the right side, the person is to do something to prevent the particle from going in on the left in the first place. In fact, this is quite easy to do: if we send a particle in from the right, it seems that it can exit on the left and deflect the incoming left-hand particle.

Carrying on our reflection in this way, we further realize that if the particle comes out on the right, we might as well send it back in order to deflect itself from entering in the first place. So all we really need to do is the following: set up a perfectly reflecting particle mirror on the right-hand side of the time travel region, and launch the particle from the left so that— if nothing interferes with it —it will just barely hit $L+$. Our paradox is now apparently complete. If, on the one hand, nothing interferes with the particle it will enter the time-travel region on the left, exit on the right, be reflected from the mirror, re-enter from the right, and come out on the left to prevent itself from ever entering. So if it enters, it gets deflected and never enters. On the other hand, if it never enters then nothing goes in on the left, so nothing comes out on the right, so nothing is reflected back, and there is nothing to deflect it from entering. So if it doesn’t enter, then there is nothing to deflect it and it enters. If it enters, then it is deflected and doesn’t enter; if it doesn’t enter then there is nothing to deflect it and it enters: paradox complete.

But at least one solution to the supposed paradox is easy to construct: just follow the recipe for constructing the minimal solution, continuing the initial trajectory of the particle (reflecting it the mirror in the obvious way) and then read of the number and trajectories of the particles from the resulting diagram. We get the result of figure 6 :

Figure 6: Resolving the “Paradox”. [An extended description of figure 6 is in the supplement.]

As we can see, the particle approaching from the left never reaches $L+$: it is deflected first by a particle which emerges from $L-$. But it is not deflected by itself , as the paradox suggests, it is deflected by another particle. Indeed, there are now four particles in the diagram: the original particle and three particles which are confined to closed time-like curves. It is not the leftmost particle which is reflected by the mirror, nor even the particle which deflects the leftmost particle; it is another particle altogether.

The paradox gets it traction from an incorrect presupposition. If there is only one particle in the world at $S$ then there is only one particle which could participate in an interaction in the time travel region: the single particle would have to interact with its earlier (or later) self. But there is no telling what might come out of $L-$: the only requirement is that whatever comes out must match what goes in at $L+$. So if you go to the trouble of constructing a working time machine, you should be prepared for a different kind of disappointment when you attempt to go back and kill yourself: you may be prevented from entering the machine in the first place by some completely unpredictable entity which emerges from it. And once again a peculiar sort of indeterminism appears: if there are many self-consistent things which could prevent you from entering, there is no telling which is even likely to materialize. This is just like the case of the unwritten book: the book is never written, so nothing determines what fills its pages.

So when the freedom to put data on $L-$ outweighs the constraint that the same data go into $L+$, instead of paradox we get an embarrassment of riches: many solution consistent with the data on $S$, or many possible books. To see a case where the constraint “outweighs” the freedom, we need to construct a very particular, and frankly artificial, dynamics and topology. Consider the space of all linear dynamics for a scalar field on a lattice. (The lattice can be though of as a simple discrete space-time.) We will depict the space-time lattice as a directed graph. There is to be a scalar field defined at every node of the graph, whose value at a given node depends linearly on the values of the field at nodes which have arrows which lead to it. Each edge of the graph can be assigned a weighting factor which determines how much the field at the input node contributes to the field at the output node. If we name the nodes by the letters a , b , c , etc., and the edges by their endpoints in the obvious way, then we can label the weighting factors by the edges they are associated with in an equally obvious way.

Suppose that the graph of the space-time lattice is acyclic , as in figure 7 . (A graph is Acyclic if one can not travel in the direction of the arrows and go in a loop.)

Figure 7: An Acyclic Lattice. [An extended description of figure 7 is in the supplement.]

It is easy to regard a set of nodes as the analog of a Cauchy surface, e.g., the set $\{a, b, c\}$, and it is obvious if arbitrary data are put on those nodes the data will generate a unique solution in the future. [ 3 ] If the value of the field at node $a$ is 3 and at node $b$ is 7, then its value at node $d$ will be $3W_{ad}$ and its value at node $e$ will be $3W_{ae} + 7W_{be}$. By varying the weighting factors we can adjust the dynamics, but in an acyclic graph the future evolution of the field will always be unique.

Let us now again artificially alter the topology of the lattice to admit CTCs, so that the graph now is cyclic. One of the simplest such graphs is depicted in figure 8 : there are now paths which lead from $z$ back to itself, e.g., $z$ to $y$ to $z$.

Figure 8: Time Travel on a Lattice. [An extended description of figure 8 is in the supplement.]

Can we now put arbitrary data on $v$ and $w$, and continue that data to a global solution? Will the solution be unique?

In the generic case, there will be a solution and the solution will be unique. The equations for the value of the field at $x, y$, and $z$ are:

Solving these equations for $z$ yields

which gives a unique value for $z$ in the generic case. But looking at the space of all possible dynamics for this lattice (i.e., the space of all possible weighting factors), we find a singularity in the case where $1-W_{zx}W_{xz} - W_{zy}W_{yz} = 0$. If we choose weighting factors in just this way, then arbitrary data at $v$ and $w$ cannot be continued to a global solution. Indeed, if the scalar field is everywhere non-negative, then this particular choice of dynamics puts ironclad constraints on the value of the field at $v$ and $w$: the field there must be zero (assuming $W_{vx}$ and $W_{wy}$ to be non-zero), and similarly all nodes in their past must have field value zero. If the field can take negative values, then the values at $v$ and $w$ must be so chosen that $vW_{vx}W_{xz} = -wW_{wy}W_{yz}$. In either case, the field values at $v$ and $w$ are severely constrained by the existence of the CTC region even though these nodes lie completely to the past of that region. It is this sort of constraint which we find to be unlike anything which appears in standard physics.

Our toy models suggest three things. The first is that it may be impossible to prove in complete generality that arbitrary data on a partial Cauchy surface can always be continued to a global solution: our artificial case provides an example where it cannot. The second is that such odd constraints are not likely to be generic: we had to delicately fine-tune the dynamics to get a problem. The third is that the opposite problem, namely data on a partial Cauchy surface being consistent with many different global solutions, is likely to be generic: we did not have to do any fine-tuning to get this result.

This third point leads to a peculiar sort of indeterminism, illustrated by the case of the unwritten book: the entire state on $S$ does not determine what will happen in the future even though the local dynamics is deterministic and there are no other “edges” to space-time from which data could influence the result. What happens in the time travel region is constrained but not determined by what happens on $S$, and the dynamics does not even supply any probabilities for the various possibilities. The example of the photographic negative discussed in section 2, then, seems likely to be unusual, for in that case there is a unique fixed point for the dynamics, and the set-up plus the dynamical laws determine the outcome. In the generic case one would rather expect multiple fixed points, with no room for anything to influence, even probabilistically, which would be realized. (See the supplement on

Remarks and Limitations on the Toy Models .

It is ironic that time travel should lead generically not to contradictions or to constraints (in the normal region) but to underdetermination of what happens in the time travel region by what happens everywhere else (an underdetermination tied neither to a probabilistic dynamics nor to a free edge to space-time). The traditional objection to time travel is that it leads to contradictions: there is no consistent way to complete an arbitrarily constructed story about how the time traveler intends to act. Instead, though, it appears that the more significant problem is underdetermination: the story can be consistently completed in many different ways.

Echeverria, Klinkhammer, and Thorne (1991) considered the case of 3-dimensional single hard spherical ball that can go through a single time travel wormhole so as to collide with its younger self.

Figure 9 [An extended description of figure 9 is in the supplement.]

The threat of paradox in this case arises in the following form. Consider the initial trajectory of a ball as it approaches the time travel region. For some initial trajectories, the ball does not undergo a collision before reaching mouth 1, but upon exiting mouth 2 it will collide with its earlier self. This leads to a contradiction if the collision is strong enough to knock the ball off its trajectory and deflect it from entering mouth 1. Of course, the Wheeler-Feynman strategy is to look for a “glancing blow” solution: a collision which will produce exactly the (small) deviation in trajectory of the earlier ball that produces exactly that collision. Are there always such solutions? [ 4 ]

Echeverria, Klinkhammer & Thorne found a large class of initial trajectories that have consistent “glancing blow” continuations, and found none that do not (but their search was not completely general). They did not produce a rigorous proof that every initial trajectory has a consistent continuation, but suggested that it is very plausible that every initial trajectory has a consistent continuation. That is to say, they have made it very plausible that, in the billiard ball wormhole case, the time travel structure of such a wormhole space-time does not result in constraints on states on spacelike surfaces in the non-time travel region.

In fact, as one might expect from our discussion in the previous section, they found the opposite problem from that of inconsistency: they found underdetermination. For a large class of initial trajectories there are multiple different consistent “glancing blow” continuations of that trajectory (many of which involve multiple wormhole traversals). For example, if one initially has a ball that is traveling on a trajectory aimed straight between the two mouths, then one obvious solution is that the ball passes between the two mouths and never time travels. But another solution is that the younger ball gets knocked into mouth 1 exactly so as to come out of mouth 2 and produce that collision. Echeverria et al. do not note the possibility (which we pointed out in the previous section) of the existence of additional balls in the time travel region. We conjecture (but have no proof) that for every initial trajectory of $A$ there are some, and generically many, multiple-ball continuations.

Friedman, Morris, et al. (1990) examined the case of source-free non-self-interacting scalar fields traveling through such a time travel wormhole and found that no constraints on initial conditions in the non-time travel region are imposed by the existence of such time travel wormholes. In general there appear to be no known counter examples to the claim that in “somewhat realistic” time-travel space-times with a partial Cauchy surface there are no constraints imposed on the state on such a partial Cauchy surface by the existence of CTC’s. (See, e.g., Friedman & Morris 1991; Thorne 1994; Earman 1995; Earman, Smeenk, & Wüthrich 2009; and Dowe 2007.)

How about the issue of constraints in the time travel region $T$? Prima facie , constraints in such a region would not appear to be surprising. But one might still expect that there should be no constraints on states on a spacelike surface, provided one keeps the surface “small enough”. In the physics literature the following question has been asked: for any point $p$ in $T$, and any space-like surface $S$ that includes $p$ is there a neighborhood $E$ of $p$ in $S$ such that any solution on $E$ can be extended to a solution on the whole space-time? With respect to this question, there are some simple models in which one has this kind of extendability of local solutions to global ones, and some simple models in which one does not have such extendability, with no clear general pattern. The technical mathematical problems are amplified by the more conceptual problem of what it might mean to say that one could create a situation which forces the creation of closed timelike curves. (See, e.g., Yurtsever 1990; Friedman, Morris, et al. 1990; Novikov 1992; Earman 1995; and Earman, Smeenk, & Wüthrich 2009). What are we to think of all of this?

The toy models above all treat billiard balls, fields, and other objects propagating through a background spacetime with CTCs. Even if we can show that a consistent solution exists, there is a further question: what kind of matter and dynamics could generate CTCs to begin with? There are various solutions of Einstein’s equations with CTCs, but how do these exotic spacetimes relate to the models actually used in describing the world? In other words, what positive reasons might we have to take CTCs seriously as a feature of the actual universe, rather than an exotic possibility of primarily mathematical interest?

We should distinguish two different kinds of “possibility” that we might have in mind in posing such questions (following Stein 1970). First, we can consider a solution as a candidate cosmological model, describing the (large-scale gravitational degrees of freedom of the) entire universe. The case for ruling out spacetimes with CTCs as potential cosmological models strikes us as, surprisingly, fairly weak. Physicists used to simply rule out solutions with CTCs as unreasonable by fiat, due to the threat of paradoxes, which we have dismantled above. But it is also challenging to make an observational case. Observations tell us very little about global features, such as the existence of CTCs, because signals can only reach an observer from a limited region of spacetime, called the past light cone. Our past light cone—and indeed the collection of all the past light cones for possible observers in a given spacetime—can be embedded in spacetimes with quite different global features (Malament 1977, Manchak 2009). This undercuts the possibility of using observations to constrain global topology, including (among other things) ruling out the existence of CTCs.

Yet the case in favor of taking cosmological models with CTCs seriously is also not particularly strong. Some solutions used to describe black holes, which are clearly relevant in a variety of astrophysical contexts, include CTCs. But the question of whether the CTCs themselves play an essential representational role is subtle: the CTCs arise in the maximal extensions of these solutions, and can plausibly be regarded as extraneous to successful applications. Furthermore, many of the known solutions with CTCs have symmetries, raising the possibility that CTCs are not a stable or robust feature. Slight departures from symmetry may lead to a solution without CTCs, suggesting that the CTCs may be an artifact of an idealized model.

The second sense of possibility regards whether “reasonable” initial conditions can be shown to lead to, or not to lead to, the formation of CTCs. As with the toy models above, suppose that we have a partial Cauchy surface $S$, such that all the temporal funny business lies to the future. Rather than simply assuming that there is a region with CTCs to the future, we can ask instead whether it is possible to create CTCs by manipulating matter in the initial, well-behaved region—that is, whether it is possible to build a time machine. Several physicists have pursued “chronology protection theorems” aiming to show that the dynamics of general relativity (or some other aspects of physics) rules this out, and to clarify why this is the case. The proof of such a theorem would justify neglecting solutions with CTCs as a source of insight into the nature of time in the actual world. But as of yet there are several partial results that do not fully settle the question. One further intriguing possibility is that even if general relativity by itself does protect chronology, it may not be possible to formulate a sensible theory describing matter and fields in solutions with CTCs. (See SEP entry on Time Machines; Smeenk and Wüthrich 2011 for more.)

There is a different question regarding the limitations of these toy models. The toy models and related examples show that there are consistent solutions for simple systems in the presence of CTCs. As usual we have made the analysis tractable by building toy models, selecting only a few dynamical degrees of freedom and tracking their evolution. But there is a large gap between the systems we have described and the time travel stories they evoke, with Kurt traveling along a CTC with murderous intentions. In particular, many features of the manifest image of time are tied to the thermodynamical properties of macroscopic systems. Rovelli (unpublished) considers a extremely simple system to illustrate the problem: can a clock move along a CTC? A clock consists of something in periodic motion, such as a pendulum bob, and something that counts the oscillations, such as an escapement mechanism. The escapement mechanism cannot work without friction; this requires dissipation and increasing entropy. For a clock that counts oscillations as it moves along a time-like trajectory, the entropy must be a monotonically increasing function. But that is obviously incompatible with the clock returning to precisely the same state at some future time as it completes a loop. The point generalizes, obviously, to imply that anything like a human, with memory and agency, cannot move along a CTC.

Since it is not obvious that one can rid oneself of all constraints in realistic models, let us examine the argument that time travel is implausible, and we should think it unlikely to exist in our world, in so far as it implies such constraints. The argument goes something like the following. In order to satisfy such constraints one needs some pre-established divine harmony between the global (time travel) structure of space-time and the distribution of particles and fields on space-like surfaces in it. But it is not plausible that the actual world, or any world even remotely like ours, is constructed with divine harmony as part of the plan. In fact, one might argue, we have empirical evidence that conditions in any spatial region can vary quite arbitrarily. So we have evidence that such constraints, whatever they are, do not in fact exist in our world. So we have evidence that there are no closed time-like lines in our world or one remotely like it. We will now examine this argument in more detail by presenting four possible responses, with counterresponses, to this argument.

Response 1. There is nothing implausible or new about such constraints. For instance, if the universe is spatially closed, there has to be enough matter to produce the needed curvature, and this puts constraints on the matter distribution on a space-like hypersurface. Thus global space-time structure can quite unproblematically constrain matter distributions on space-like hypersurfaces in it. Moreover we have no realistic idea what these constraints look like, so we hardly can be said to have evidence that they do not obtain.

Counterresponse 1. Of course there are constraining relations between the global structure of space-time and the matter in it. The Einstein equations relate curvature of the manifold to the matter distribution in it. But what is so strange and implausible about the constraints imposed by the existence of closed time-like curves is that these constraints in essence have nothing to do with the Einstein equations. When investigating such constraints one typically treats the particles and/or field in question as test particles and/or fields in a given space-time, i.e., they are assumed not to affect the metric of space-time in any way. In typical space-times without closed time-like curves this means that one has, in essence, complete freedom of matter distribution on a space-like hypersurface. (See response 2 for some more discussion of this issue). The constraints imposed by the possibility of time travel have a quite different origin and are implausible. In the ordinary case there is a causal interaction between matter and space-time that results in relations between global structure of space-time and the matter distribution in it. In the time travel case there is no such causal story to be told: there simply has to be some pre-established harmony between the global space-time structure and the matter distribution on some space-like surfaces. This is implausible.

Response 2. Constraints upon matter distributions are nothing new. For instance, Maxwell’s equations constrain electric fields $\boldsymbol{E}$ on an initial surface to be related to the (simultaneous) charge density distribution $\varrho$ by the equation $\varrho = \text{div}(\boldsymbol{E})$. (If we assume that the $E$ field is generated solely by the charge distribution, this conditions amounts to requiring that the $E$ field at any point in space simply be the one generated by the charge distribution according to Coulomb’s inverse square law of electrostatics.) This is not implausible divine harmony. Such constraints can hold as a matter of physical law. Moreover, if we had inferred from the apparent free variation of conditions on spatial regions that there could be no such constraints we would have mistakenly inferred that $\varrho = \text{div}(\boldsymbol{E})$ could not be a law of nature.

Counterresponse 2. The constraints imposed by the existence of closed time-like lines are of quite a different character from the constraint imposed by $\varrho = \text{div}(\boldsymbol{E})$. The constraints imposed by $\varrho = \text{div}(\boldsymbol{E})$ on the state on a space-like hypersurface are:

local constraints (i.e., to check whether the constraint holds in a region you just need to see whether it holds at each point in the region),
quite independent of the global space-time structure,
quite independent of how the space-like surface in question is embedded in a given space-time, and
very simply and generally stateable.

On the other hand, the consistency constraints imposed by the existence of closed time-like curves (i) are not local, (ii) are dependent on the global structure of space-time, (iii) depend on the location of the space-like surface in question in a given space-time, and (iv) appear not to be simply stateable other than as the demand that the state on that space-like surface embedded in such and such a way in a given space-time, do not lead to inconsistency. On some views of laws (e.g., David Lewis’ view) this plausibly implies that such constraints, even if they hold, could not possibly be laws. But even if one does not accept such a view of laws, one could claim that the bizarre features of such constraints imply that it is implausible that such constraints hold in our world or in any world remotely like ours.

Response 3. It would be strange if there are constraints in the non-time travel region. It is not strange if there are constraints in the time travel region. They should be explained in terms of the strange, self-interactive, character of time travel regions. In this region there are time-like trajectories from points to themselves. Thus the state at such a point, in such a region, will, in a sense, interact with itself. It is a well-known fact that systems that interact with themselves will develop into an equilibrium state, if there is such an equilibrium state, or else will develop towards some singularity. Normally, of course, self-interaction isn’t true instantaneous self-interaction, but consists of a feed-back mechanism that takes time. But in time travel regions something like true instantaneous self-interaction occurs. This explains why constraints on states occur in such time travel regions: the states “ ab initio ” have to be “equilibrium states”. Indeed in a way this also provides some picture of why indeterminism occurs in time travel regions: at the onset of self-interaction states can fork into different equi-possible equilibrium states.

Counterresponse 3. This is explanation by woolly analogy. It all goes to show that time travel leads to such bizarre consequences that it is unlikely that it occurs in a world remotely like ours.

Response 4. All of the previous discussion completely misses the point. So far we have been taking the space-time structure as given, and asked the question whether a given time travel space-time structure imposes constraints on states on (parts of) space-like surfaces. However, space-time and matter interact. Suppose that one is in a space-time with closed time-like lines, such that certain counterfactual distributions of matter on some neighborhood of a point $p$ are ruled out if one holds that space-time structure fixed. One might then ask

Why does the actual state near $p$ in fact satisfy these constraints? By what divine luck or plan is this local state compatible with the global space-time structure? What if conditions near $p$ had been slightly different?

And one might take it that the lack of normal answers to these questions indicates that it is very implausible that our world, or any remotely like it, is such a time travel universe. However the proper response to these question is the following. There are no constraints in any significant sense. If they hold they hold as a matter of accidental fact, not of law. There is no more explanation of them possible than there is of any contingent fact. Had conditions in a neighborhood of $p$ been otherwise, the global structure of space-time would have been different. So what? The only question relevant to the issue of constraints is whether an arbitrary state on an arbitrary spatial surface $S$ can always be embedded into a space-time such that that state on $S$ consistently extends to a solution on the entire space-time.

But we know the answer to that question. A well-known theorem in general relativity says the following: any initial data set on a three dimensional manifold $S$ with positive definite metric has a unique embedding into a maximal space-time in which $S$ is a Cauchy surface (see, e.g., Geroch & Horowitz 1979: 284 for more detail), i.e., there is a unique largest space-time which has $S$ as a Cauchy surface and contains a consistent evolution of the initial value data on $S$. Now since $S$ is a Cauchy surface this space-time does not have closed time like curves. But it may have extensions (in which $S$ is not a Cauchy surface) which include closed timelike curves, indeed it may be that any maximal extension of it would include closed timelike curves. (This appears to be the case for extensions of states on certain surfaces of Taub-NUT space-times. See Earman, Smeenk, & Wüthrich 2009). But these extensions, of course, will be consistent. So properly speaking, there are no constraints on states on space-like surfaces. Nonetheless the space-time in which these are embedded may or may not include closed time-like curves.

Counterresponse 4. This, in essence, is the stonewalling answer which we indicated in section 1. However, whether or not you call the constraints imposed by a given space-time on distributions of matter on certain space-like surfaces “genuine constraints”, whether or not they can be considered lawlike, and whether or not they need to be explained, the existence of such constraints can still be used to argue that time travel worlds are so bizarre that it is implausible that our world or any world remotely like ours is a time travel world.

Suppose that one is in a time travel world. Suppose that given the global space-time structure of this world, there are constraints imposed upon, say, the state of motion of a ball on some space-like surface when it is treated as a test particle, i.e., when it is assumed that the ball does not affect the metric properties of the space-time it is in. (There is lots of other matter that, via the Einstein equation, corresponds exactly to the curvature that there is everywhere in this time travel worlds.) Now a real ball of course does have some effect on the metric of the space-time it is in. But let us consider a ball that is so small that its effect on the metric is negligible. Presumably it will still be the case that certain states of this ball on that space-like surface are not compatible with the global time travel structure of this universe.

This means that the actual distribution of matter on such a space-like surface can be extended into a space-time with closed time-like lines, but that certain counterfactual distributions of matter on this space-like surface can not be extended into the same space-time. But note that the changes made in the matter distribution (when going from the actual to the counterfactual distribution) do not in any non-negligible way affect the metric properties of the space-time. (Recall that the changes only effect test particles.) Thus the reason why the global time travel properties of the counterfactual space-time have to be significantly different from the actual space-time is not that there are problems with metric singularities or alterations in the metric that force significant global changes when we go to the counterfactual matter distribution. The reason that the counterfactual space-time has to be different is that in the counterfactual world the ball’s initial state of motion starting on the space-like surface, could not “meet up” in a consistent way with its earlier self (could not be consistently extended) if we were to let the global structure of the counterfactual space-time be the same as that of the actual space-time. Now, it is not bizarre or implausible that there is a counterfactual dependence of manifold structure, even of its topology, on matter distributions on spacelike surfaces. For instance, certain matter distributions may lead to singularities, others may not. We may indeed in some sense have causal power over the topology of the space-time we live in. But this power normally comes via the Einstein equations. But it is bizarre to think that there could be a counterfactual dependence of global space-time structure on the arrangement of certain tiny bits of matter on some space-like surface, where changes in that arrangement by assumption do not affect the metric anywhere in space-time in any significant way . It is implausible that we live in such a world, or that a world even remotely like ours is like that.

Let us illustrate this argument in a different way by assuming that wormhole time travel imposes constraints upon the states of people prior to such time travel, where the people have so little mass/energy that they have negligible effect, via the Einstein equation, on the local metric properties of space-time. Do you think it more plausible that we live in a world where wormhole time travel occurs but it only occurs when people’s states are such that these local states happen to combine with time travel in such a way that nobody ever succeeds in killing their younger self, or do you think it more plausible that we are not in a wormhole time travel world? [ 5 ]

An alternative approach to time travel (initiated by Deutsch 1991) abstracts away from the idealized toy models described above. [ 6 ] This computational approach considers instead the evolution of bits (simple physical systems with two discrete states) through a network of interactions, which can be represented by a circuit diagram with gates corresponding to the interactions. Motivated by the possibility of CTCs, Deutsch proposed adding a new kind of channel that connects the output of a given gate back to its input —in essence, a backwards-time step. More concretely, given a gate that takes $n$ bits as input, we can imagine taking some number $i \lt n$ of these bits through a channel that loops back and then do double-duty as inputs. Consistency requires that the state of these $i$ bits is the same for output and input. (We will consider an illustration of this kind of system in the next section.) Working through examples of circuit diagrams with a CTC channel leads to similar treatments of Consistency and Underdetermination as the discussion above (see, e.g., Wallace 2012: § 10.6). But the approach offers two new insights (both originally due to Deutsch): the Easy Knowledge paradox, and a particularly clear extension to time travel in quantum mechanics.

A computer equipped with a CTC channel can exploit the need to find consistent evolution to solve remarkably hard problems. (This is quite different than the first idea that comes to mind to enhance computational power: namely to just devote more time to a computation, and then send the result back on the CTC to an earlier state.) The gate in a circuit incorporating a CTC implements a function from the input bits to the output bits, under the constraint that the output and input match the i bits going through the CTC channel. This requires, in effect, finding the fixed point of the relevant function. Given the generality of the model, there are few limits on the functions that could be implemented on the CTC circuit. Nature has to solve a hard computational problem just to ensure consistent evolution. This can then be extended to other complex computational problems—leading, more precisely, to solutions of NP -complete problems in polynomial time (see Aaronson 2013: Chapter 20 for an overview and further references). The limits imposed by computational complexity are an essential part of our epistemic situation, and computers with CTCs would radically change this.

We now turn to the application of the computational approach to the quantum physics of time travel (see Deutsch 1991; Deutsch & Lockwood 1994). By contrast with the earlier discussions of constraints in classical systems, they claim to show that time travel never imposes any constraints on the pre-time travel state of quantum systems. The essence of this account is as follows. [ 7 ]

A quantum system starts in state $S_1$, interacts with its older self, after the interaction is in state $S_2$, time travels while developing into state $S_3$, then interacts with its younger self, and ends in state $S_4$ (see figure 10 ).

Figure 10 [An extended description of figure 10 is in the supplement.]

Deutsch assumes that the set of possible states of this system are the mixed states, i.e., are represented by the density matrices over the Hilbert space of that system. Deutsch then shows that for any initial state $S_1$, any unitary interaction between the older and younger self, and any unitary development during time travel, there is a consistent solution, i.e., there is at least one pair of states $S_2$ and $S_3$ such that when $S_1$ interacts with $S_3$ it will change to state $S_2$ and $S_2$ will then develop into $S_3$. The states $S_2, S_3$ and $S_4$ will typically be not be pure states, i.e., will be non-trivial mixed states, even if $S_1$ is pure. In order to understand how this leads to interpretational problems let us give an example. Consider a system that has a two dimensional Hilbert space with as a basis the states $\vc{+}$ and $\vc{-}$. Let us suppose that when state $\vc{+}$ of the young system encounters state $\vc{+}$ of the older system, they interact and the young system develops into state $\vc{-}$ and the old system remains in state $\vc{+}$. In obvious notation:

Similarly, suppose that:

Let us furthermore assume that there is no development of the state of the system during time travel, i.e., that $\vc{+}_2$ develops into $\vc{+}_3$, and that $\vc{-}_2$ develops into $\vc{-}_3$.

Now, if the only possible states of the system were $\vc{+}$ and $\vc{-}$ (i.e., if there were no superpositions or mixtures of these states), then there is a constraint on initial states: initial state $\vc{+}_1$ is impossible. For if $\vc{+}_1$ interacts with $\vc{+}_3$ then it will develop into $\vc{-}_2$, which, during time travel, will develop into $\vc{-}_3$, which inconsistent with the assumed state $\vc{+}_3$. Similarly if $\vc{+}_1$ interacts with $\vc{-}_3$ it will develop into $\vc{+}_2$, which will then develop into $\vc{+}_3$ which is also inconsistent. Thus the system can not start in state $\vc{+}_1$.

But, says Deutsch, in quantum mechanics such a system can also be in any mixture of the states $\vc{+}$ and $\vc{-}$. Suppose that the older system, prior to the interaction, is in a state $S_3$ which is an equal mixture of 50% $\vc{+}_3$ and 50% $\vc{-}_3$. Then the younger system during the interaction will develop into a mixture of 50% $\vc{+}_2$ and 50% $\vc{-}_2$, which will then develop into a mixture of 50% $\vc{+}_3$ and 50% $\vc{-}_3$, which is consistent! More generally Deutsch uses a fixed point theorem to show that no matter what the unitary development during interaction is, and no matter what the unitary development during time travel is, for any state $S_1$ there is always a state $S_3$ (which typically is not a pure state) which causes $S_1$ to develop into a state $S_2$ which develops into that state $S_3$. Thus quantum mechanics comes to the rescue: it shows in all generality that no constraints on initial states are needed!

One might wonder why Deutsch appeals to mixed states: will superpositions of states $\vc{+}$ and $\vc{-}$ not suffice? Unfortunately such an idea does not work. Suppose again that the initial state is $\vc{+}_1$. One might suggest that that if state $S_3$ is

one will obtain a consistent development. For one might think that when initial state $\vc{+}_1$ encounters the superposition

it will develop into superposition

and that this in turn will develop into

as desired. However this is not correct. For initial state $\vc{+}_1$ when it encounters

will develop into the entangled state

In so far as one can speak of the state of the young system after this interaction, it is in the mixture of 50% $\vc{+}_2$ and 50% $\vc{-}_2$, not in the superposition

So Deutsch does need his recourse to mixed states.

This clarification of why Deutsch needs his mixtures does however indicate a serious worry about the simplifications that are part of Deutsch’s account. After the interaction the old and young system will (typically) be in an entangled state. Although for purposes of a measurement on one of the two systems one can say that this system is in a mixed state, one can not represent the full state of the two systems by specifying the mixed state of each separate part, as there are correlations between observables of the two systems that are not represented by these two mixed states, but are represented in the joint entangled state. But if there really is an entangled state of the old and young systems directly after the interaction, how is one to represent the subsequent development of this entangled state? Will the state of the younger system remain entangled with the state of the older system as the younger system time travels and the older system moves on into the future? On what space-like surfaces are we to imagine this total entangled state to be? At this point it becomes clear that there is no obvious and simple way to extend elementary non-relativistic quantum mechanics to space-times with closed time-like curves: we apparently need to characterize not just the entanglement between two systems, but entanglement relative to specific spacetime descriptions.

How does Deutsch avoid these complications? Deutsch assumes a mixed state $S_3$ of the older system prior to the interaction with the younger system. He lets it interact with an arbitrary pure state $S_1$ younger system. After this interaction there is an entangled state $S'$ of the two systems. Deutsch computes the mixed state $S_2$ of the younger system which is implied by this entangled state $S'$. His demand for consistency then is just that this mixed state $S_2$ develops into the mixed state $S_3$. Now it is not at all clear that this is a legitimate way to simplify the problem of time travel in quantum mechanics. But even if we grant him this simplification there is a problem: how are we to understand these mixtures?

If we take an ignorance interpretation of mixtures we run into trouble. For suppose that we assume that in each individual case each older system is either in state $\vc{+}_3$ or in state $\vc{-}_3$ prior to the interaction. Then we regain our paradox. Deutsch instead recommends the following, many worlds, picture of mixtures. Suppose we start with state $\vc{+}_1$ in all worlds. In some of the many worlds the older system will be in the $\vc{+}_3$ state, let us call them A -worlds, and in some worlds, B -worlds, it will be in the $\vc{-}_3$ state. Thus in A -worlds after interaction we will have state $\vc{-}_2$ , and in B -worlds we will have state $\vc{+}_2$. During time travel the $\vc{-}_2$ state will remain the same, i.e., turn into state $\vc{-}_3$, but the systems in question will travel from A -worlds to B -worlds. Similarly the $\vc{+}$ $_2$ states will travel from the B -worlds to the A -worlds, thus preserving consistency.

Now whatever one thinks of the merits of many worlds interpretations, and of this understanding of it applied to mixtures, in the end one does not obtain genuine time travel in Deutsch’s account. The systems in question travel from one time in one world to another time in another world, but no system travels to an earlier time in the same world. (This is so at least in the normal sense of the word “world”, the sense that one means when, for instance, one says “there was, and will be, only one Elvis Presley in this world.”) Thus, even if it were a reasonable view, it is not quite as interesting as it may have initially seemed. (See Wallace 2012 for a more sympathetic treatment, that explores several further implications of accepting time travel in conjunction with the many worlds interpretation.)

We close by acknowledging that Deutsch’s starting point—the claim that this computational model captures the essential features of quantum systems in a spacetime with CTCs—has been the subject of some debate. Several physicists have pursued a quite different treatment of evolution of quantum systems through CTC’s, based on considering the “post-selected” state (see Lloyd et al. 2011). Their motivations for implementing the consistency condition in terms of the post-selected state reflects a different stance towards quantum foundations. A different line of argument aims to determine whether Deutsch’s treatment holds as an appropriate limiting case of a more rigorous treatment, such as quantum field theory in curved spacetimes. For example, Verch (2020) establishes several results challenging the assumption that Deutsch’s treatment is tied to the presence of CTC’s, or that it is compatible with the entanglement structure of quantum fields.

What remains of the grandfather paradox in general relativistic time travel worlds is the fact that in some cases the states on edgeless spacelike surfaces are “overconstrained”, so that one has less than the usual freedom in specifying conditions on such a surface, given the time-travel structure, and in some cases such states are “underconstrained”, so that states on edgeless space-like surfaces do not determine what happens elsewhere in the way that they usually do, given the time travel structure. There can also be mixtures of those two types of cases. The extent to which states are overconstrained and/or underconstrained in realistic models is as yet unclear, though it would be very surprising if neither obtained. The extant literature has primarily focused on the problem of overconstraint, since that, often, either is regarded as a metaphysical obstacle to the possibility time travel, or as an epistemological obstacle to the plausibility of time travel in our world. While it is true that our world would be quite different from the way we normally think it is if states were overconstrained, underconstraint seems at least as bizarre as overconstraint. Nonetheless, neither directly rules out the possibility of time travel.

If time travel entailed contradictions then the issue would be settled. And indeed, most of the stories employing time travel in popular culture are logically incoherent: one cannot “change” the past to be different from what it was, since the past (like the present and the future) only occurs once. But if the only requirement demanded is logical coherence, then it seems all too easy. A clever author can devise a coherent time-travel scenario in which everything happens just once and in a consistent way. This is just too cheap: logical coherence is a very weak condition, and many things we take to be metaphysically impossible are logically coherent. For example, it involves no logical contradiction to suppose that water is not molecular, but if both chemistry and Kripke are right it is a metaphysical impossibility. We have been interested not in logical possibility but in physical possibility. But even so, our conditions have been relatively weak: we have asked only whether time-travel is consistent with the universal validity of certain fundamental physical laws and with the notion that the physical state on a surface prior to the time travel region be unconstrained. It is perfectly possible that the physical laws obey this condition, but still that time travel is not metaphysically possible because of the nature of time itself. Consider an analogy. Aristotle believed that water is homoiomerous and infinitely divisible: any bit of water could be subdivided, in principle, into smaller bits of water. Aristotle’s view contains no logical contradiction. It was certainly consistent with Aristotle’s conception of water that it be homoiomerous, so this was, for him, a conceptual possibility. But if chemistry is right, Aristotle was wrong both about what water is like and what is possible for it. It can’t be infinitely divided, even though no logical or conceptual analysis would reveal that.

Similarly, even if all of our consistency conditions can be met, it does not follow that time travel is physically possible, only that some specific physical considerations cannot rule it out. The only serious proof of the possibility of time travel would be a demonstration of its actuality. For if we agree that there is no actual time travel in our universe, the supposition that there might have been involves postulating a substantial difference from actuality, a difference unlike in kind from anything we could know if firsthand. It is unclear to us exactly what the content of possible would be if one were to either maintain or deny the possibility of time travel in these circumstances, unless one merely meant that the possibility is not ruled out by some delineated set of constraints. As the example of Aristotle’s theory of water shows, conceptual and logical “possibility” do not entail possibility in a full-blooded sense. What exactly such a full-blooded sense would be in case of time travel, and whether one could have reason to believe it to obtain, remain to us obscure.

Aaronson, Scott, 2013, Quantum Computing since Democritus , Cambridge: Cambridge University Press. doi:10.1017/CBO9780511979309
Arntzenius, Frank, 2006, “Time Travel: Double Your Fun”, Philosophy Compass , 1(6): 599–616. doi:10.1111/j.1747-9991.2006.00045.x
Clarke, C.J.S., 1977, “Time in General Relativity” in Foundations of Space-Time Theory , Minnesota Studies in the Philosophy of Science , Vol VIII, Earman, J., Glymour, C., and Stachel, J. (eds), pp. 94–108. Minneapolis: University of Minnesota Press.
Deutsch, David, 1991, “Quantum Mechanics near Closed Timelike Lines”, Physical Review D , 44(10): 3197–3217. doi:10.1103/PhysRevD.44.3197
Deutsch, David and Michael Lockwood, 1994, “The Quantum Physics of Time Travel”, Scientific American , 270(3): 68–74. doi:10.1038/scientificamerican0394-68
Dowe, Phil, 2007, “Constraints on Data in Worlds with Closed Timelike Curves”, Philosophy of Science , 74(5): 724–735. doi:10.1086/525617
Earman, John, 1972, “Implications of Causal Propagation Outside the Null Cone”, Australasian Journal of Philosophy , 50(3): 222–237. doi:10.1080/00048407212341281
Earman, John, 1995, Bangs, Crunches, Whimpers, and Shrieks: Singularities and Acausalities in Relativistic Spacetimes , New York: Oxford University Press.
Earman, John, Christopher Smeenk, and Christian Wüthrich, 2009, “Do the Laws of Physics Forbid the Operation of Time Machines?”, Synthese , 169(1): 91–124. doi:10.1007/s11229-008-9338-2
Echeverria, Fernando, Gunnar Klinkhammer, and Kip S. Thorne, 1991, “Billiard Balls in Wormhole Spacetimes with Closed Timelike Curves: Classical Theory”, Physical Review D , 44(4): 1077–1099. doi:10.1103/PhysRevD.44.1077
Effingham, Nikk, 2020, Time Travel: Probability and Impossibility , Oxford: Oxford University Press. doi:10.1093/oso/9780198842507.001.0001
Fletcher, Samuel C., 2020, “The Principle of Stability”, Philosopher’s Imprint , 20: article 3. [ Fletcher 2020 available online ]
Friedman, John and Michael Morris, 1991, “The Cauchy Problem for the Scalar Wave Equation Is Well Defined on a Class of Spacetimes with Closed Timelike Curves”, Physical Review Letters , 66(4): 401–404. doi:10.1103/PhysRevLett.66.401
Friedman, John, Michael S. Morris, Igor D. Novikov, Fernando Echeverria, Gunnar Klinkhammer, Kip S. Thorne, and Ulvi Yurtsever, 1990, “Cauchy Problem in Spacetimes with Closed Timelike Curves”, Physical Review D , 42(6): 1915–1930. doi:10.1103/PhysRevD.42.1915
Geroch, Robert and Gary Horowitz, 1979, “Global Structures of Spacetimes”, in General Relativity: An Einstein Centenary Survey , Stephen Hawking and W. Israel (eds.), Cambridge/New York: Cambridge University Press, Chapter 5, pp. 212–293.
Gödel, Kurt, 1949, “A Remark About the Relationship Between Relativity Theory and Idealistic Philosophy”, in Albert Einstein, Philosopher-Scientist , Paul Arthur Schilpp (ed.), Evanston, IL: Library of Living Philosophers, 557–562.
Hocking, John G. and Gail S. Young, 1961, Topology , (Addison-Wesley Series in Mathematics), Reading, MA: Addison-Wesley.
Horwich, Paul, 1987, “Time Travel”, in his Asymmetries in Time: Problems in the Philosophy of Science , , Cambridge, MA: MIT Press, 111–128.
Kutach, Douglas N., 2003, “Time Travel and Consistency Constraints”, Philosophy of Science , 70(5): 1098–1113. doi:10.1086/377392
Lewis, David, 1976, “The Paradoxes of Time Travel”, American Philosophical Quarterly , 13(2): 145–152.
Lloyd, Seth, Lorenzo Maccone, Raul Garcia-Patron, Vittorio Giovannetti, and Yutaka Shikano, 2011, “Quantum Mechanics of Time Travel through Post-Selected Teleportation”, Physical Review D , 84(2): 025007. doi:10.1103/PhysRevD.84.025007
Malament, David B., 1977, “Observationally Indistinguishable Spacetimes: Comments on Glymour’s Paper”, in Foundations of Space-Time Theories , John Earman, Clark N. Glymour, and John J. Stachel (eds.), (Minnesota Studies in the Philosophy of Science 8), Minneapolis, MN: University of Minnesota Press, 61–80.
–––, 1984, “‘Time Travel’ in the Gödel Universe”, PSA: Proceedings of the Biennial Meeting of the Philosophy of Science Association , 1984(2): 91–100. doi:10.1086/psaprocbienmeetp.1984.2.192497
–––, 1985, “Minimal Acceleration Requirements for ‘Time Travel’, in Gödel Space‐time”, Journal of Mathematical Physics , 26(4): 774–777. doi:10.1063/1.526566
Manchak, John Byron, 2009, “Can We Know the Global Structure of Spacetime?”, Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics , 40(1): 53–56. doi:10.1016/j.shpsb.2008.07.004
–––, 2011, “On Efficient ‘Time Travel’ in Gödel Spacetime”, General Relativity and Gravitation , 43(1): 51–60. doi:10.1007/s10714-010-1068-3
Maudlin, Tim, 1990, “Time-Travel and Topology”, PSA: Proceedings of the Biennial Meeting of the Philosophy of Science Association , 1990(1): 303–315. doi:10.1086/psaprocbienmeetp.1990.1.192712
Novikov, I. D., 1992, “Time Machine and Self-Consistent Evolution in Problems with Self-Interaction”, Physical Review D , 45(6): 1989–1994. doi:10.1103/PhysRevD.45.1989
Smeenk, Chris and Christian Wüthrich, 2011, “Time Travel and Time Machines”, in the Oxford Handbook on Time , Craig Callender (ed.), Oxford: Oxford University Press, 577–630..
Stein, Howard, 1970, “On the Paradoxical Time-Structures of Gödel”, Philosophy of Science , 37(4): 589–601. doi:10.1086/288328
Thorne, Kip S., 1994, Black Holes and Time Warps: Einstein’s Outrageous Legacy , (Commonwealth Fund Book Program), New York: W.W. Norton.
Verch, Rainer, 2020, “The D-CTC Condition in Quantum Field Theory”, in Progress and Visions in Quantum Theory in View of Gravity , Felix Finster, Domenico Giulini, Johannes Kleiner, and Jürgen Tolksdorf (eds.), Cham: Springer International Publishing, 221–232. doi:10.1007/978-3-030-38941-3_9
Wallace, David, 2012, The Emergent Multiverse: Quantum Theory According to the Everett Interpretation , Oxford: Oxford University Press. doi:10.1093/acprof:oso/9780199546961.001.0001
Wasserman, Ryan, 2018, Paradoxes of Time Travel , Oxford: Oxford University Press. doi:10.1093/oso/9780198793335.001.0001
Weyl, Hermann, 1918/1920 [1922/1952], Raum, Zeit, Materie , Berlin: Springer; fourth edition 1920. Translated as Space—Time—Matter , Henry Leopold Brose (trans.), New York: Dutton, 1922. Reprinted 1952, New York: Dover Publications.
Wheeler, John Archibald and Richard Phillips Feynman, 1949, “Classical Electrodynamics in Terms of Direct Interparticle Action”, Reviews of Modern Physics , 21(3): 425–433. doi:10.1103/RevModPhys.21.425
Yurtsever, Ulvi, 1990, “Test Fields on Compact Space‐times”, Journal of Mathematical Physics , 31(12): 3064–3078. doi:10.1063/1.528960

How to cite this entry . Preview the PDF version of this entry at the Friends of the SEP Society . Look up topics and thinkers related to this entry at the Internet Philosophy Ontology Project (InPhO). Enhanced bibliography for this entry at PhilPapers , with links to its database.

Adlam, Emily, unpublished, “ Is There Causation in Fundamental Physics? New Insights from Process Matrices and Quantum Causal Modelling ”, 2022, arXiv: 2208.02721. doi:10.48550/ARXIV.2208.02721
Rovelli, Carlo, unpublished, “ Can We Travel to the Past? Irreversible Physics along Closed Timelike Curves ”, arXiv: 1912.04702. doi:10.48550/ARXIV.1912.04702

Accessibility

Support SEP

Mirror sites.

View this site from another server:

Info about mirror sites

Library of Congress Catalog Data: ISSN 1095-5054

Search Menu
Browse content in Arts and Humanities
Browse content in Archaeology
Anglo-Saxon and Medieval Archaeology
Archaeological Methodology and Techniques
Archaeology by Region
Archaeology of Religion
Archaeology of Trade and Exchange
Biblical Archaeology
Contemporary and Public Archaeology
Environmental Archaeology
Historical Archaeology
History and Theory of Archaeology
Industrial Archaeology
Landscape Archaeology
Mortuary Archaeology
Prehistoric Archaeology
Underwater Archaeology
Urban Archaeology
Zooarchaeology
Browse content in Architecture
Architectural Structure and Design
History of Architecture
Residential and Domestic Buildings
Theory of Architecture
Browse content in Art
Art Subjects and Themes
History of Art
Industrial and Commercial Art
Theory of Art
Biographical Studies
Byzantine Studies
Browse content in Classical Studies
Classical History
Classical Philosophy
Classical Mythology
Classical Literature
Classical Reception
Classical Art and Architecture
Classical Oratory and Rhetoric
Greek and Roman Papyrology
Greek and Roman Epigraphy
Greek and Roman Law
Greek and Roman Archaeology
Late Antiquity
Religion in the Ancient World
Digital Humanities
Browse content in History
Colonialism and Imperialism
Diplomatic History
Environmental History
Genealogy, Heraldry, Names, and Honours
Genocide and Ethnic Cleansing
Historical Geography
History by Period
History of Emotions
History of Agriculture
History of Education
History of Gender and Sexuality
Industrial History
Intellectual History
International History
Labour History
Legal and Constitutional History
Local and Family History
Maritime History
Military History
National Liberation and Post-Colonialism
Oral History
Political History
Public History
Regional and National History
Revolutions and Rebellions
Slavery and Abolition of Slavery
Social and Cultural History
Theory, Methods, and Historiography
Urban History
World History
Browse content in Language Teaching and Learning
Language Learning (Specific Skills)
Language Teaching Theory and Methods
Browse content in Linguistics
Applied Linguistics
Cognitive Linguistics
Computational Linguistics
Forensic Linguistics
Grammar, Syntax and Morphology
Historical and Diachronic Linguistics
History of English
Language Evolution
Language Reference
Language Acquisition
Language Variation
Language Families
Lexicography
Linguistic Anthropology
Linguistic Theories
Linguistic Typology
Phonetics and Phonology
Psycholinguistics
Sociolinguistics
Translation and Interpretation
Writing Systems
Browse content in Literature
Bibliography
Children's Literature Studies
Literary Studies (Romanticism)
Literary Studies (American)
Literary Studies (Asian)
Literary Studies (European)
Literary Studies (Eco-criticism)
Literary Studies (Modernism)
Literary Studies - World
Literary Studies (1500 to 1800)
Literary Studies (19th Century)
Literary Studies (20th Century onwards)
Literary Studies (African American Literature)
Literary Studies (British and Irish)
Literary Studies (Early and Medieval)
Literary Studies (Fiction, Novelists, and Prose Writers)
Literary Studies (Gender Studies)
Literary Studies (Graphic Novels)
Literary Studies (History of the Book)
Literary Studies (Plays and Playwrights)
Literary Studies (Poetry and Poets)
Literary Studies (Postcolonial Literature)
Literary Studies (Queer Studies)
Literary Studies (Science Fiction)
Literary Studies (Travel Literature)
Literary Studies (War Literature)
Literary Studies (Women's Writing)
Literary Theory and Cultural Studies
Mythology and Folklore
Shakespeare Studies and Criticism
Browse content in Media Studies
Browse content in Music
Applied Music
Dance and Music
Ethics in Music
Ethnomusicology
Gender and Sexuality in Music
Medicine and Music
Music Cultures
Music and Media
Music and Religion
Music and Culture
Music Education and Pedagogy
Music Theory and Analysis
Musical Scores, Lyrics, and Libretti
Musical Structures, Styles, and Techniques
Musicology and Music History
Performance Practice and Studies
Race and Ethnicity in Music
Sound Studies
Browse content in Performing Arts
Browse content in Philosophy
Aesthetics and Philosophy of Art
Epistemology
Feminist Philosophy
History of Western Philosophy
Metaphysics
Moral Philosophy
Non-Western Philosophy
Philosophy of Language
Philosophy of Mind
Philosophy of Perception
Philosophy of Science
Philosophy of Action
Philosophy of Law
Philosophy of Religion
Philosophy of Mathematics and Logic
Practical Ethics
Social and Political Philosophy
Browse content in Religion
Biblical Studies
Christianity
East Asian Religions
History of Religion
Judaism and Jewish Studies
Qumran Studies
Religion and Education
Religion and Health
Religion and Politics
Religion and Science
Religion and Law
Religion and Art, Literature, and Music
Religious Studies
Browse content in Society and Culture
Cookery, Food, and Drink
Cultural Studies
Customs and Traditions
Ethical Issues and Debates
Hobbies, Games, Arts and Crafts
Lifestyle, Home, and Garden
Natural world, Country Life, and Pets
Popular Beliefs and Controversial Knowledge
Sports and Outdoor Recreation
Technology and Society
Travel and Holiday
Visual Culture
Browse content in Law
Arbitration
Browse content in Company and Commercial Law
Commercial Law
Company Law
Browse content in Comparative Law
Systems of Law
Competition Law
Browse content in Constitutional and Administrative Law
Government Powers
Judicial Review
Local Government Law
Military and Defence Law
Parliamentary and Legislative Practice
Construction Law
Contract Law
Browse content in Criminal Law
Criminal Procedure
Criminal Evidence Law
Sentencing and Punishment
Employment and Labour Law
Environment and Energy Law
Browse content in Financial Law
Banking Law
Insolvency Law
History of Law
Human Rights and Immigration
Intellectual Property Law
Browse content in International Law
Private International Law and Conflict of Laws
Public International Law
IT and Communications Law
Jurisprudence and Philosophy of Law
Law and Politics
Law and Society
Browse content in Legal System and Practice
Courts and Procedure
Legal Skills and Practice
Primary Sources of Law
Regulation of Legal Profession
Medical and Healthcare Law
Browse content in Policing
Criminal Investigation and Detection
Police and Security Services
Police Procedure and Law
Police Regional Planning
Browse content in Property Law
Personal Property Law
Study and Revision
Terrorism and National Security Law
Browse content in Trusts Law
Wills and Probate or Succession
Browse content in Medicine and Health
Browse content in Allied Health Professions
Arts Therapies
Clinical Science
Dietetics and Nutrition
Occupational Therapy
Operating Department Practice
Physiotherapy
Radiography
Speech and Language Therapy
Browse content in Anaesthetics
General Anaesthesia
Neuroanaesthesia
Clinical Neuroscience
Browse content in Clinical Medicine
Acute Medicine
Cardiovascular Medicine
Clinical Genetics
Clinical Pharmacology and Therapeutics
Dermatology
Endocrinology and Diabetes
Gastroenterology
Genito-urinary Medicine
Geriatric Medicine
Infectious Diseases
Medical Toxicology
Medical Oncology
Pain Medicine
Palliative Medicine
Rehabilitation Medicine
Respiratory Medicine and Pulmonology
Rheumatology
Sleep Medicine
Sports and Exercise Medicine
Community Medical Services
Critical Care
Emergency Medicine
Forensic Medicine
Haematology
History of Medicine
Browse content in Medical Skills
Clinical Skills
Communication Skills
Nursing Skills
Surgical Skills
Browse content in Medical Dentistry
Oral and Maxillofacial Surgery
Paediatric Dentistry
Restorative Dentistry and Orthodontics
Surgical Dentistry
Medical Ethics
Medical Statistics and Methodology
Browse content in Neurology
Clinical Neurophysiology
Neuropathology
Nursing Studies
Browse content in Obstetrics and Gynaecology
Gynaecology
Occupational Medicine
Ophthalmology
Otolaryngology (ENT)
Browse content in Paediatrics
Neonatology
Browse content in Pathology
Chemical Pathology
Clinical Cytogenetics and Molecular Genetics
Histopathology
Medical Microbiology and Virology
Patient Education and Information
Browse content in Pharmacology
Psychopharmacology
Browse content in Popular Health
Caring for Others
Complementary and Alternative Medicine
Self-help and Personal Development
Browse content in Preclinical Medicine
Cell Biology
Molecular Biology and Genetics
Reproduction, Growth and Development
Primary Care
Professional Development in Medicine
Browse content in Psychiatry
Addiction Medicine
Child and Adolescent Psychiatry
Forensic Psychiatry
Learning Disabilities
Old Age Psychiatry
Psychotherapy
Browse content in Public Health and Epidemiology
Epidemiology
Public Health
Browse content in Radiology
Clinical Radiology
Interventional Radiology
Nuclear Medicine
Radiation Oncology
Reproductive Medicine
Browse content in Surgery
Cardiothoracic Surgery
Gastro-intestinal and Colorectal Surgery
General Surgery
Neurosurgery
Paediatric Surgery
Peri-operative Care
Plastic and Reconstructive Surgery
Surgical Oncology
Transplant Surgery
Trauma and Orthopaedic Surgery
Vascular Surgery
Browse content in Science and Mathematics
Browse content in Biological Sciences
Aquatic Biology
Biochemistry
Bioinformatics and Computational Biology
Developmental Biology
Ecology and Conservation
Evolutionary Biology
Genetics and Genomics
Microbiology
Molecular and Cell Biology
Natural History
Plant Sciences and Forestry
Research Methods in Life Sciences
Structural Biology
Systems Biology
Zoology and Animal Sciences
Browse content in Chemistry
Analytical Chemistry
Computational Chemistry
Crystallography
Environmental Chemistry
Industrial Chemistry
Inorganic Chemistry
Materials Chemistry
Medicinal Chemistry
Mineralogy and Gems
Organic Chemistry
Physical Chemistry
Polymer Chemistry
Study and Communication Skills in Chemistry
Theoretical Chemistry
Browse content in Computer Science
Artificial Intelligence
Computer Architecture and Logic Design
Game Studies
Human-Computer Interaction
Mathematical Theory of Computation
Programming Languages
Software Engineering
Systems Analysis and Design
Virtual Reality
Browse content in Computing
Business Applications
Computer Security
Computer Games
Computer Networking and Communications
Digital Lifestyle
Graphical and Digital Media Applications
Operating Systems
Browse content in Earth Sciences and Geography
Atmospheric Sciences
Environmental Geography
Geology and the Lithosphere
Maps and Map-making
Meteorology and Climatology
Oceanography and Hydrology
Palaeontology
Physical Geography and Topography
Regional Geography
Soil Science
Urban Geography
Browse content in Engineering and Technology
Agriculture and Farming
Biological Engineering
Civil Engineering, Surveying, and Building
Electronics and Communications Engineering
Energy Technology
Engineering (General)
Environmental Science, Engineering, and Technology
History of Engineering and Technology
Mechanical Engineering and Materials
Technology of Industrial Chemistry
Transport Technology and Trades
Browse content in Environmental Science
Applied Ecology (Environmental Science)
Conservation of the Environment (Environmental Science)
Environmental Sustainability
Environmentalist Thought and Ideology (Environmental Science)
Management of Land and Natural Resources (Environmental Science)
Natural Disasters (Environmental Science)
Nuclear Issues (Environmental Science)
Pollution and Threats to the Environment (Environmental Science)
Social Impact of Environmental Issues (Environmental Science)
History of Science and Technology
Browse content in Materials Science
Ceramics and Glasses
Composite Materials
Metals, Alloying, and Corrosion
Nanotechnology
Browse content in Mathematics
Applied Mathematics
Biomathematics and Statistics
History of Mathematics
Mathematical Education
Mathematical Finance
Mathematical Analysis
Numerical and Computational Mathematics
Probability and Statistics
Pure Mathematics
Browse content in Neuroscience
Cognition and Behavioural Neuroscience
Development of the Nervous System
Disorders of the Nervous System
History of Neuroscience
Invertebrate Neurobiology
Molecular and Cellular Systems
Neuroendocrinology and Autonomic Nervous System
Neuroscientific Techniques
Sensory and Motor Systems
Browse content in Physics
Astronomy and Astrophysics
Atomic, Molecular, and Optical Physics
Biological and Medical Physics
Classical Mechanics
Computational Physics
Condensed Matter Physics
Electromagnetism, Optics, and Acoustics
History of Physics
Mathematical and Statistical Physics
Measurement Science
Nuclear Physics
Particles and Fields
Plasma Physics
Quantum Physics
Relativity and Gravitation
Semiconductor and Mesoscopic Physics
Browse content in Psychology
Affective Sciences
Clinical Psychology
Cognitive Psychology
Cognitive Neuroscience
Criminal and Forensic Psychology
Developmental Psychology
Educational Psychology
Evolutionary Psychology
Health Psychology
History and Systems in Psychology
Music Psychology
Neuropsychology
Organizational Psychology
Psychological Assessment and Testing
Psychology of Human-Technology Interaction
Psychology Professional Development and Training
Research Methods in Psychology
Social Psychology
Browse content in Social Sciences
Browse content in Anthropology
Anthropology of Religion
Human Evolution
Medical Anthropology
Physical Anthropology
Regional Anthropology
Social and Cultural Anthropology
Theory and Practice of Anthropology
Browse content in Business and Management
Business Ethics
Business Strategy
Business History
Business and Technology
Business and Government
Business and the Environment
Comparative Management
Corporate Governance
Corporate Social Responsibility
Entrepreneurship
Health Management
Human Resource Management
Industrial and Employment Relations
Industry Studies
Information and Communication Technologies
International Business
Knowledge Management
Management and Management Techniques
Operations Management
Organizational Theory and Behaviour
Pensions and Pension Management
Public and Nonprofit Management
Strategic Management
Supply Chain Management
Browse content in Criminology and Criminal Justice
Criminal Justice
Criminology
Forms of Crime
International and Comparative Criminology
Youth Violence and Juvenile Justice
Development Studies
Browse content in Economics
Agricultural, Environmental, and Natural Resource Economics
Asian Economics
Behavioural Finance
Behavioural Economics and Neuroeconomics
Econometrics and Mathematical Economics
Economic History
Economic Systems
Economic Methodology
Economic Development and Growth
Financial Markets
Financial Institutions and Services
General Economics and Teaching
Health, Education, and Welfare
History of Economic Thought
International Economics
Labour and Demographic Economics
Law and Economics
Macroeconomics and Monetary Economics
Microeconomics
Public Economics
Urban, Rural, and Regional Economics
Welfare Economics
Browse content in Education
Adult Education and Continuous Learning
Care and Counselling of Students
Early Childhood and Elementary Education
Educational Equipment and Technology
Educational Strategies and Policy
Higher and Further Education
Organization and Management of Education
Philosophy and Theory of Education
Schools Studies
Secondary Education
Teaching of a Specific Subject
Teaching of Specific Groups and Special Educational Needs
Teaching Skills and Techniques
Browse content in Environment
Applied Ecology (Social Science)
Climate Change
Conservation of the Environment (Social Science)
Environmentalist Thought and Ideology (Social Science)
Natural Disasters (Environment)
Social Impact of Environmental Issues (Social Science)
Browse content in Human Geography
Cultural Geography
Economic Geography
Political Geography
Browse content in Interdisciplinary Studies
Communication Studies
Museums, Libraries, and Information Sciences
Browse content in Politics
African Politics
Asian Politics
Chinese Politics
Comparative Politics
Conflict Politics
Elections and Electoral Studies
Environmental Politics
European Union
Foreign Policy
Gender and Politics
Human Rights and Politics
Indian Politics
International Relations
International Organization (Politics)
International Political Economy
Irish Politics
Latin American Politics
Middle Eastern Politics
Political Behaviour
Political Economy
Political Institutions
Political Methodology
Political Communication
Political Philosophy
Political Sociology
Political Theory
Politics and Law
Public Policy
Public Administration
Quantitative Political Methodology
Regional Political Studies
Russian Politics
Security Studies
State and Local Government
UK Politics
US Politics
Browse content in Regional and Area Studies
African Studies
Asian Studies
East Asian Studies
Japanese Studies
Latin American Studies
Middle Eastern Studies
Native American Studies
Scottish Studies
Browse content in Research and Information
Research Methods
Browse content in Social Work
Addictions and Substance Misuse
Adoption and Fostering
Care of the Elderly
Child and Adolescent Social Work
Couple and Family Social Work
Developmental and Physical Disabilities Social Work
Direct Practice and Clinical Social Work
Emergency Services
Human Behaviour and the Social Environment
International and Global Issues in Social Work
Mental and Behavioural Health
Social Justice and Human Rights
Social Policy and Advocacy
Social Work and Crime and Justice
Social Work Macro Practice
Social Work Practice Settings
Social Work Research and Evidence-based Practice
Welfare and Benefit Systems
Browse content in Sociology
Childhood Studies
Community Development
Comparative and Historical Sociology
Economic Sociology
Gender and Sexuality
Gerontology and Ageing
Health, Illness, and Medicine
Marriage and the Family
Migration Studies
Occupations, Professions, and Work
Organizations
Population and Demography
Race and Ethnicity
Social Theory
Social Movements and Social Change
Social Research and Statistics
Social Stratification, Inequality, and Mobility
Sociology of Religion
Sociology of Education
Sport and Leisure
Urban and Rural Studies
Browse content in Warfare and Defence
Defence Strategy, Planning, and Research
Land Forces and Warfare
Military Administration
Military Life and Institutions
Naval Forces and Warfare
Other Warfare and Defence Issues
Peace Studies and Conflict Resolution
Weapons and Equipment

Paradoxes of Time Travel

Professor of Philosophy

Cite Icon Cite
Permissions Icon Permissions

Paradoxes of Time Travel is a comprehensive study of the philosophical issues raised by the possibility of time travel. The book begins, in Chapter 1, by explaining the concept of time travel and clarifying the central question to be addressed: Is time travel compatible with the laws of metaphysics and, in particular, the laws concerning time, freedom, causation, and identity? Chapter 2 then explores the various temporal paradoxes, including the double-occupancy problem, the no-destination argument, and the famous twin paradox of special relativity. Chapters 3 and 4 focus on the paradoxes of freedom, including various versions of the grandfather paradox. Chapter 5 covers causal paradoxes, including the bootstrapping paradox, the problems of backward causation, and the various puzzles raised by causal loops. Chapter 6 then concludes by looking at various paradoxes of identity. This includes a discussion of different theories of change and persistence, and an exploration of the various puzzles raised by self-visitation.

Signed in as

Institutional accounts.

GoogleCrawler [DO NOT DELETE]
Google Scholar Indexing

Personal account

Sign in with email/username & password
Get email alerts
Save searches
Purchase content
Activate your purchase/trial code

Institutional access

Sign in with a library card Sign in with username/password Recommend to your librarian
Institutional account management
Get help with access

Access to content on Oxford Academic is often provided through institutional subscriptions and purchases. If you are a member of an institution with an active account, you may be able to access content in one of the following ways:

IP based access

Typically, access is provided across an institutional network to a range of IP addresses. This authentication occurs automatically, and it is not possible to sign out of an IP authenticated account.

Sign in through your institution

Choose this option to get remote access when outside your institution. Shibboleth/Open Athens technology is used to provide single sign-on between your institutionâ€™s website and Oxford Academic.

Click Sign in through your institution.
Select your institution from the list provided, which will take you to your institution's website to sign in.
When on the institution site, please use the credentials provided by your institution. Do not use an Oxford Academic personal account.
Following successful sign in, you will be returned to Oxford Academic.

If your institution is not listed or you cannot sign in to your institutionâ€™s website, please contact your librarian or administrator.

Sign in with a library card

Enter your library card number to sign in. If you cannot sign in, please contact your librarian.

Society Members

Society member access to a journal is achieved in one of the following ways:

Sign in through society site

Many societies offer single sign-on between the society website and Oxford Academic. If you see â€˜Sign in through society siteâ€™ in the sign in pane within a journal:

Click Sign in through society site.
When on the society site, please use the credentials provided by that society. Do not use an Oxford Academic personal account.

If you do not have a society account or have forgotten your username or password, please contact your society.

Sign in using a personal account

Some societies use Oxford Academic personal accounts to provide access to their members. See below.

A personal account can be used to get email alerts, save searches, purchase content, and activate subscriptions.

Some societies use Oxford Academic personal accounts to provide access to their members.

Viewing your signed in accounts

Click the account icon in the top right to:

View your signed in personal account and access account management features.
View the institutional accounts that are providing access.

Signed in but can't access content

Oxford Academic is home to a wide variety of products. The institutional subscription may not cover the content that you are trying to access. If you believe you should have access to that content, please contact your librarian.

For librarians and administrators, your personal account also provides access to institutional account management. Here you will find options to view and activate subscriptions, manage institutional settings and access options, access usage statistics, and more.

Our books are available by subscription or purchase to libraries and institutions.

About Oxford Academic
Publish journals with us
University press partners
What we publish
New features
Open access
Rights and permissions
Accessibility
Advertising
Media enquiries
Oxford University Press
Oxford Languages
University of Oxford

Oxford University Press is a department of the University of Oxford. It furthers the University's objective of excellence in research, scholarship, and education by publishing worldwide

Copyright © 2024 Oxford University Press
Cookie settings
Cookie policy
Privacy policy
Legal notice

This Feature Is Available To Subscribers Only

This PDF is available to Subscribers Only

For full access to this pdf, sign in to an existing account, or purchase an annual subscription.

University of Notre Dame

Notre Dame Philosophical Reviews

Home ›
Reviews ›

Paradoxes of Time Travel

Ryan Wasserman, Paradoxes of Time Travel , Oxford University Press, 2018, 240pp., $60.00, ISBN 9780198793335.

Reviewed by John W. Carroll, North Carolina State

Wasserman's book fills a gap in the academic literature on time travel. The gap was hidden among the journal articles on time travel written by physicists for physicists, the popular books on time travel by physicists for the curious folk, the books on the history of time travel in science fiction intended for a range of scholarly audiences, and the journal articles on time travel written for and by metaphysicians and philosophers of science. There are metaphysics books on time that give some attention to time travel, but, as far as I know, this is the first book length work devoted to the topic of time travel by a metaphysician homed in on the most important metaphysical issues. Wasserman addresses these issues while still managing to include pertinent scientific discussion and enjoyable time-travel snippets from science fiction. The book is well organized and is suitable for good undergraduate metaphysics students, for philosophy graduate students, and for professional philosophers. It reads like a sophisticated and excellent textbook even though it includes many novel ideas.

The research Wasserman has done is impressive. It reminds the reader that time travel as a topic of metaphysics did not start with David Lewis (1976). Wasserman (p. 2 n 4) identifies Walter B. Pitkin's 1914 journal article as (probably) the first academic discussion of time travel. The article includes a description of what has come to be called the double-occupancy problem, a puzzle about spatial location and time machines that trace a continuous path through space. The same note also includes a lovely passage, which anticipates paradoxes about changing the past, from Enrique Gaspar's 1887 book:

We may unwrap time but we don't know how to nullify it. If today is a consequence of yesterday and we are living examples of the present, we cannot unless we destroy ourselves, wipe out a cause of which we are the actual effects.

These are just two of the many useful bits of Wasserman's research.

Chapter 1 usefully introduces examples of time travel and some examples one might think would involve time travel, but do not (e.g., changing time zones). There is good discussion of Lewis's definition of time travel as a discrepancy between personal and external time, including a brief passage (p. 13) from a previously unpublished letter from Lewis to Jonathan Bennett on whether freezing and thawing is time travel. I had often wonder what Lewis would have said; now I know what he did say!

Chapter 2 dives into temporal paradoxes deriving from discussions of the status of tense and the ontology of time (presentism vs. eternalism vs. growing block vs. . . . ). Here, Wasserman also includes the double-occupancy problem as a problem for eternalism -- though it is not clear that it is only a problem for eternalism. Then he turns to the question of the compatibility of presentism and time travel, the compatibility of time travel and a version of growing block that accepts that there are no future-tensed truths, and finally to a section on relativity and time travel. The section on relativity is solid and seems to me to pull the rug out from under some earlier discussions. For example, Lewis's definition of time travel is shown not to work. It also becomes clear that presentism and the growing block are consistent with both time-dilation-style forward time travel and traveling-in-a-curved-spacetime "backwards" time travel.

Chapters 3 and 4 cover the granddaddies of all the time-travel paradoxes: the freedom paradoxes that include the grandfather paradox, the possibility of changing the past, and the prospects of such changes given models of branching time, models that invoke parallel worlds, and hyper time models. Chapter 4 gets serious about Lewis's treatment of the grandfather paradox and Kadri Vihvelin's treatment of the autoinfanticide paradox (about which I will have more to say).

Chapter 4 also includes discussion of "mechanical" paradoxes that, as stated, do not require modal premises about what something can and cannot do, and no notion of freedom or free will. (See Earman's bilking argument on p. 139 and the Polchinski paradox on p. 141.) Wasserman introduces modality to these paradoxes, but I would have liked them to be addressed on their own terms. As I see it, these paradoxes are introduced to show that backwards time travel or backwards causation in a certain situation validly lead to a contradiction. On their own terms, for these arguments to be valid, the premises of the arguments themselves must be inconsistent. How can one make trouble for backwards time travel if the argument is thus bound to be unsound?

Chapter 5 takes on the paradoxes generated by causal loops or more generally backwards causation including bilking arguments, the boot-strapping paradox (based on a presumption that self-causation is impossible), and the ex nihilo paradox with causal loops and object loops (i.e., jinn) that seem to have no cause or explanation.

Chapter 6 deals with paradoxes that arise from considerations regarding identity, with a focus on the self-visitation paradox from both perdurantist and endurantist perspectives. I was surprised to learn that Wasserman had defended an endurantist-friendly property compatibilism -- similar to my own -- to resolve the self-visitation paradox. I was then delighted to find out that he cleverly extends this sort of compatibilism to the time-travel-free problem of change (i.e., the so-called, temporary-intrinsics argument).

The outstanding scientific issue regarding backwards time travel is whether it is physically possible. There is no question that forwards time travel is actual, or even whether it is ubiquitous. There is also not much question that backwards time travel is consistent with general relativity. Still, we await more scientific progress before we will know whether backwards time travel really is consistent with the actual laws of nature. In the meantime, there is still much to be said about Lewis's treatment of the grandfather paradox and Vihvelin's stated challenge to that treatment in terms of the autoinfanticide paradox.

I will start by being somewhat critical of Lewis's approach. For his part (pp. 108-114), Wasserman does a terrific job of laying out Lewis's position as a metatheoretic discussion of the context sensitivity of 'can' and 'can't'. My concern is that not enough attention is given to the 'can' and 'can't' sentences that turn out true on the semantics. The semantics works only by a contextual restriction of possible worlds based on relevant facts -- the modal base -- associated with a conversational context. In meager contexts, false 'can' sentences will turn out true too easily. For example, suppose two people are having a conversation about Roger. Maybe all the two know about Roger is his name and that he is moving into the neighborhood. So, the proposition that Roger doesn't play the piano is not in the modal base. So, according to Lewis's semantics applied to 'can', 'Roger can play the piano' is true in this context. That seems wrong. This would be an unwarranted assertion for either of the participants in the conversation to make. Notice it is also true relative to the same meager context that Roger can play the harpsichord, the sousaphone, and the nyatiti. Quite a musician that Roger! [1]

Interestingly, though this problem arises for 'can', it does not arise for other "possibility" modals. For example, notice that, with the meager context described above, there is a big difference regarding the assertability of 'Roger could play the piano' and of 'Roger can play the piano'. Similarly, there is also no serious issue with regard to 'Roger might play the piano'. 'Could' and 'might' add tentativeness to the assertion that seems called for. There also seems to be no problem for the semantics insofar as it applies to 'is possible'. 'It is possible that Roger plays the piano' rings true relative to the context. But 'Roger can play the piano'? That shouldn't turn out true, especially if Roger is physically or psychologically unsuited for piano playing.

This issue has been frustrating for me, but Wasserman's book has me leaning toward the idea that what is needed is a contextual semantics that includes a distinguishing conditional treatment of 'can' of the sort Wasserman suggests:

(P1**) Necessarily, if someone would fail to do something no matter what she tried, then she cannot do it (p. 122).

This is a suggestion made by Wasserman on behalf of Vihvelin. I find (P1**) as a promising place to start in terms of the conditional treatment.

Speaking of Vihvelin, her thesis is "that no time traveler can kill the baby that in fact is her younger self, given what we ordinarily mean by 'can'" (1996, pp. 316-317). Vihvelin cites Paul Horwich as a defender of a can-kill solution, what she calls the standard reply :

The standard reply . . . goes something like this: Of course the time traveler . . . will not kill the baby who is her younger self . . . But that doesn't mean she can't . (Vihvelin 1996, p. 315)

Vihvelin's doing so is appropriate given what Horwich says about Charles attending the Battle of Hastings: "From the fact that someone did not do something it does not follow that he was not free to do it" (1975, 435). In contrast, it strikes me as odd that Vihvelin (1996, p. 329, fn. 1) also attributes the standard reply to Lewis. I presume that she does so based on some comments by Lewis. He says, "By any ordinary standards of ability , Tim can kill Grandfather," (1976, p. 150, my emphasis) and especially "what, in an ordinary sense , I can do" (1976, p. 151, my emphasis). So, admittedly, Vihvelin fairly highlights an aspect of Lewis's view as holding that, in the ordinary sense of 'can', Tim can kill Gramps. And I can see how this is a useful presentation of Lewis's position for her argumentative purposes.

Nevertheless, I take Lewis's talk of ordinary standards or an ordinary sense to just be a way to identify the ordinary contexts that arise with uses of 'can' in day-to-day dealings, where the possibility of time travel is not even on the table. Simple stuff like:

Hey, can you reach the pencil that fell on the floor?

Sure I can; here it is.

More importantly, we have to keep in mind that the basic semantics only has consequences about the truth of 'can' sentences once a modal base is in place. To me, the fact that Baby Suzy grows up to be Suzy is exactly the kind of fact that we do not ordinarily hold fixed. Lewis's commitment to the semantics does not make him either a can-kill guy or a can't-kill guy.

What is the upshot of this? There is a bit of underappreciation of Lewis's approach in Wasserman's discussion of Vihvelin's views. The pinching case on p. 119 provides a way to make the point. Consider:

(a) If Suzy were to try to kill Baby Suzy, then she would fail.

(b) If Suzy were to try to pinch Baby Suzy, then she would fail.

According to Wasserman, Vihvelin thinks that even in ordinary contexts (a) and (b) come apart (p. 119, note 32) -- (a) is true and (b) is false. As I see it, a natural context for (a) includes the fact that Baby Suzy grows up normally to be Suzy. That is a supposition that is crucial to the description of the scenario and so is likely to be part of the modal base. No canonical story or suppositions are tied to (b), though Vihvelin stipulates that Suzy travels back in time in both cases. We are not, however, told a story of Baby Suzy living a pinch-free life all the way to adulthood. We are not told whether Suzy decided go back in time because Baby Suzy deserved a pinch for some past transgression. My point is that the stories affect the context. So, with parallel background stories, (a) and (b) need not come apart.

I am not sure whether Wasserman was speaking for himself or for Vihvelin when he says about (a) and (b), "Self-defeating acts are paradoxical in a way other past-altering acts are not" (p. 120). Either way, I disagree. Lewis gives a more general way to resolve the past-alteration paradoxes that is not obviously in any serious conflict with Vihvelin's many utterances that turn out true relative to the contexts in which she asserts them. Wasserman also says, "The only disagreement between Lewis and Vihvelin is over whether Suzy's killing Baby Suzy is compatible with the kinds of facts we normally take as relevant in determining what someone can do" (p. 117). That is an odd thing for him to say. Lewis sketches a semantic theory that provides a framework for the truth conditions of 'can' and 'can't' sentences. He is not in disagreement with Vihvelin. For Lewis, there is one specification of truth conditions for 'can' that gives rise to both 'can kill' and 'can't kill' sentences turning out true relative to different contexts. Indeed, it is tempting to think that Vihvelin takes the fact that Baby Suzy grows up to be Adult Suzy as part of the modal base of the contexts from which she asserts the compelling 'can't-kill' sentences.

That all said, Wasserman's book is a significant contribution. There are those of us who focus a good chunk of our research on the paradoxes of time travel for their intrinsic interest, and especially because they are fun to teach. That is contribution enough for me. But, ultimately, from this somewhat esoteric, fun puzzle solving, we also learn more about the rest of metaphysics. The traditional issues of metaphysics: identity-over-time, freedom and determinism, causation, time and space, counterfactuals, personhood, mereology, and so on, all take on a new look when framed by the questions of whether time travel is possible and what time travel is or would be like. Wasserman's book is a wonderful source that spotlights these connections between the paradoxes of time travel and more traditional metaphysical issues.

Cargile, J., 1996. "Some Comments on Fatalism" The Philosophical Quarterly 46, No. 182 January 1996, 1-11.

Gaspar, E., 1887/2012. The Time-Ship: A Chronological Journey . Wesleyan University Press.

Horwich, P., 1975. "On Some Alleged Paradoxes of Time Travel" The Journal of Philosophy 72, 432-444.

Lewis, D., 1976 "The Paradoxes of Time Travel" American Philosophical Quarterly 13, 145-152.

Pitkin, W., 1914. "Time and Pure Activity" Journal of Philosophy, Psychology and Scientific Methods 11, 521-526.

Vihvelin, K., 1996. "What a Time Traveler Cannot Do" Philosophical Studies 81, 315-330.

[1] This criticism was first presented to me by Natalja Deng in the question-and-answer period for a presentation at the 2014 Philosophy of Time Society Conference. Later on, I found a parallel challenge in work by James Cargile (1996, 10-11) about Lewis's iconic, 'The ape can't speak Finnish, but I can'.

The Magazine
Stay Curious
The Sciences
Environment
Planet Earth

How Does Multiverse Theory Relate to Time Travel?

The theoretical physics and paradoxes of time travel often brush up against multiverse theory and the idea of alternate universes..

While many sci-fi writers have wondered if time travel into the past can be allowed as long as you slip into an alternate universe, you should be warned: Nature doesn’t like a cheater.

Time travel into the past is a real pain in the neck. For one, as far as we can tell it’s forbidden in our universe. You can travel into the future as slowly or as quickly as you like, but you can’t stop time or go in reverse.

Is It Possible To Travel Back in Time?

Technically speaking, physicists are not exactly sure why time travel is forbidden. We don’t have a single law of physics that clearly rejects the possibility.

But every time we try to concoct a time travel concept — like wormholes or twisting paths around infinitely long cylinders — we find some reason that it’s not allowed. Wormholes, it turns out, require negative mass to stabilize themselves, and infinitely long cylinders are rather hard to come by.

Read More: Why Do Humans Perceive Time The Way We Do?

The Trouble With Changing the Past

Even within any glimmer of a possibility that time travel might be possible, traveling into our own pasts opens up all sorts of noxious paradoxes, as plenty of films and comic book storylines have demonstrated.

Beyond the fact that the past is over and done with, we must reckon with the reality that what happened in the past created the present that we experience.

To put the paradox succinctly: If you change the past, you change the present, but the present already exists.

The Grandfather Paradox

One of the most common examples of this head-scratching scenario is known as the grandfather paradox.

Suppose you travel back in time and kill your own grandfather before he met your grandmother (no need to dissect your motivations behind this hypothetical act here). That means one of your parents was never born, which means you never exist. But if you never existed, how did you go back in time to kill your grandfather in the first place?

Read More: What Is the Grandfather Paradox of Time Travel?

Are There Multiple Universes?

To address this dilemma, we could invoke the idea of parallel or alternate universes, a concept under the general umbrella of the multiverse.

Perhaps when you go back and kill your grandfather, you create a new universe where you don’t exist. You can then return to your original universe where everything is hunky-dory (or, at least you’re still alive). Essentially, you only monkeyed around with some other, disconnected cosmos.

There are, in fact, two places in physics where the multiverse concept pops up. Unfortunately for any wannabe time travelers, neither of them allows for this type of parallel-futures hopping.

Splitting-Off Worlds in Quantum Mechanics

The first place where alternate universe theories have gained traction is in quantum mechanics.

Subatomic processes are inherently random. When we run an experiment we never know what result we’re going to get. One explanation for this is that all experimental results happen, just in separate universes.

If someone shoves an electron through a strong magnetic field, for example, and it has a fifty-fifty chance of deflecting either up or down, then every time they run an electron through the device, they get two universes: one where the electron went up, and one where the electron went down.

As the theory goes, this kind of splitting isn’t just limited to arcane physics experiments. It happens with every single quantum interaction throughout the cosmos, which is a lot of interactions, thus generating countless parallel worlds.

In this view, there is a universe out there that already exists where your grandfather is dead and you were never born. But you could never see it.

Read More: Advanced Quantum Material Curves the Fabric of Space

No Travel Between Worlds in Quantum Mechanics

Even if the theory above is actually happening, the rules of quantum physics are absolutely clear: There is no travel or communication between these universes.

Granted, “universe” is probably the wrong word here. That’s because the splitting is really separate partitions of a single quantum wave function. And that separation is really permanent.

If there was any kind of connection allowed, then the many branching possibilities of quantum processes simply wouldn’t happen.

Bubble Universe Theory

The second place where the multiverse pops up in physics is in studies related to the extremely early universe.

From this lens, our cosmos could be just one of many — like a bubble in an infinite foam of universes. These universes too could contain all the many interesting and varied possibilities that make life so fun.

In this (extremely hypothetical) view, there are many universes out there that contain alternate realities from the one you know. There’s one where your grandfather died. There’s another where no stars ever formed. And there’s a universe where all your matter is replaced with antimatter, and so on.

Because all these bubble universes exist in the same expanding foam that is reality, those alternate universes really are out there , an unimaginable but still-finite distance away.

Time Still Marches Forward in the Multiverse

But even in this foam-like collection of bubble universes, time still does its thing. That is, it moves forward, always.

Even if you could concoct some scheme to travel among the alternate universes, those universes still share the same spacetime fabric, marching forward along with us. Thus they all appear to forbid time travel, as the theory goes.

They also, in theory, share the reality that nature doesn’t like a cheater. So, if you’re theoretically going to visit a universe where you never existed, maybe nix the time travel method.

Read More: Scientists Attempt to Map the Multiverse

subatomic particles

Already a subscriber?

Keep reading for as low as $1.99!

Save up to 40% off the cover price when you subscribe to Discover magazine.

The Grandfather Paradox: Is Time Travel Possible?

T he concept of time travel has long captivated the human imagination, inspiring countless works of science fiction and fueling speculation about the possibility of journeying backward or forward in time. One of the most famous thought experiments in the realm of time travel is the Grandfather Paradox—a hypothetical scenario in which a time traveler could potentially alter the past in a way that prevents their own existence. In this article, we will delve into the intricacies of the Grandfather Paradox, examine the challenges it poses to the concept of time travel, and explore current scientific theories and speculations regarding the feasibility of traversing the fourth dimension.

The Grandfather Paradox Explained:

The Grandfather Paradox is a classic paradoxical scenario that arises from the notion of time travel. It posits a hypothetical situation in which a person travels back in time and kills their own grandfather before their parent is conceived, thus preventing their own birth. This creates a logical contradiction—if the time traveler’s grandfather is never born, then the time traveler would never exist to travel back in time and commit the act of patricide.

Paradoxes and Causality:

The Grandfather Paradox highlights the potential contradictions and complexities inherent in the concept of time travel, particularly when it comes to causality—the relationship between cause and effect. In the context of the paradox, the time traveler’s actions in the past have the potential to alter the course of history in ways that defy conventional notions of cause and effect, leading to logical inconsistencies and paradoxical outcomes.

Temporal Mechanics and Alternate Timelines:

One proposed solution to the Grandfather Paradox is the idea of alternate timelines or parallel universes. According to this interpretation, when the time traveler alters the past, they create a new timeline or branch of reality in which their actions have different consequences. In this scenario, the original timeline remains intact, unaffected by the time traveler’s interference, while the altered timeline diverges into a separate reality with its own set of events and outcomes.

Closed Timelike Curves and Wormholes:

In theoretical physics, closed timelike curves (CTCs) are hypothetical paths through spacetime that loop back on themselves, allowing for the possibility of time travel. Wormholes, which are hypothetical tunnels or shortcuts through spacetime, have been proposed as potential mechanisms for traversing CTCs and facilitating time travel. While the existence of wormholes remains speculative, their theoretical properties raise intriguing questions about the nature of spacetime and the feasibility of time travel.

Time Dilation and Relativity:

The theory of relativity, formulated by Albert Einstein in the early 20th century, provides a theoretical framework for understanding the nature of spacetime and the effects of gravity on the passage of time. According to the theory of special relativity, time dilation occurs when an object is in motion relative to an observer, causing time to pass more slowly for the moving object. This phenomenon has been experimentally confirmed and plays a crucial role in various applications of modern physics, including GPS satellites and particle accelerators.

Quantum Mechanics and Entanglement:

Quantum mechanics, the branch of physics that describes the behavior of particles at the smallest scales, introduces additional complexities to the concept of time travel. Quantum entanglement, a phenomenon in which particles become correlated in such a way that the state of one particle instantaneously influences the state of another, raises questions about the nature of causality and the possibility of information transfer across spacetime. While quantum mechanics offers intriguing insights into the nature of reality, its implications for time travel remain speculative and subject to ongoing debate.

The Arrow of Time and Thermodynamics:

The arrow of time, which refers to the directionality of time’s flow from past to future, is intimately linked to the second law of thermodynamics, which states that entropy, or disorder, tends to increase over time. The concept of time travel raises intriguing questions about the nature of causality and the relationship between the past, present, and future. While time travel remains a staple of science fiction, its feasibility in the real world is a topic of ongoing scientific inquiry and speculation.

Philosophical Implications:

Beyond its scientific and theoretical implications, the concept of time travel raises profound philosophical questions about the nature of free will, determinism, and personal identity. The Grandfather Paradox, in particular, forces us to confront the possibility of altering the past and the implications of such actions for our own existence and the course of history. While time travel remains a tantalizing prospect, its potential consequences for the fabric of reality and the human experience are subjects of speculation and debate.

Ethical Considerations:

The prospect of time travel also raises ethical considerations regarding the potential impact of altering the past on individuals, societies, and the course of history. Questions about the responsibility of time travelers, the preservation of historical integrity, and the consequences of unintended consequences loom large in discussions of time travel ethics. As we contemplate the feasibility of time travel, it is essential to consider the ethical implications of altering the past and the potential risks and benefits associated with such endeavors.

The Search for Answers:

While the Grandfather Paradox and other paradoxes of time travel present formidable challenges to our understanding of the nature of reality, they also inspire curiosity, imagination, and inquiry. Scientists, philosophers, and science fiction authors continue to explore the mysteries of time travel, probing the boundaries of theoretical physics, metaphysics, and human imagination in search of answers to some of the most profound questions about existence, time, and the universe.

Conclusion:

The Grandfather Paradox and the concept of time travel represent a fascinating intersection of science, philosophy, and speculation. While the feasibility of time travel remains uncertain and the Grandfather Paradox poses formidable challenges to our understanding of causality and reality, the quest to unravel the mysteries of time continues to inspire curiosity and inquiry. Whether through theoretical physics, philosophical reflection, or imaginative storytelling, the exploration of time travel invites us to contemplate the nature of existence, the passage of time, and the boundless possibilities of the cosmos. As we grapple with the paradoxes and possibilities of time travel, we are reminded of the enduring human quest to unlock the secrets of the universe and journey into the unknown realms of spacetime.

Read More: Will Bitcoin Reach $100K Sooner Than Expected? Chinese Asset Managers and Hong Kong’s Major ETF Push Could Accelerate Growth

The Grandfather Paradox: Is Time Travel Possible? 2

Home → Features → Natural Sciences → Physics → Quantum Mechanics

Time Travel Without the Paradoxes

Join ZME Science in its carefully non-copyright infringing time machine with your sidekick ‘Marty’ to see if time travel paradoxes can be escaped.

It’s one of the most popular ideas in fiction — travelling back through time to alter the course of history. The idea of travelling through time — more than we do every day that is — isn’t just the remit of science fiction writers though. Many physicists have also considered the plausibility of time travel, especially since Einstein’s theory of special relativity changed our concept of what time actually is.

Yet, as many science fiction epics warn, such a journey through time could carry with it some heavy consequences.

Ray Bradbury’s short story ‘A Sound of Thunder’ centres around a group of time travellers who blunder into prehistory, making changes that have horrendous repercussions for their world. In an even more horrific example of a paradox, during an award-winning episode of the animated sci-fi sitcom Futurama, the series’ hapless hero Fry travels back in the past and in the ultimate grandfather paradox , kills his supposed gramps. Then, after ‘encounter’ with his grandmother, Fry realises why he hasn’t faded from reality, he is his own grandfather. Many theorists have also considered methods of time travel without the risk of paradox. Techniques that don’t require the rather extreme measure of getting overly friendly with one’s own grandmother Fry. These paradox-escape mechanisms range from aspects of mathematics to interpretations of quantum weirdness.

Before looking at those paradox escape plans it’s worth examining just how special relativity changed our thinking about time, and why it started theoretical physicists really thinking about time travel. Luckily at ZME Science, we have a pleasingly non-copyright infringing time machine to travel back to the past. Let’s step into this strange old phone booth, take a trip to the 80s to pick up Marty and then journey back to 1905, the year Albert Einstein published ‘ Zur Elektrodynamik bewegter Körper’ or ‘On the Electrodynamics of Moving Bodies.’ The paper that gave birth to special relativity. Don’t worry Marty… You’ll be home before you know it… Probably.

A Trip to 1905: Einstein’s Spacetime is Born

As Marty reads the chronometer and discovers that we have arrived in 1905, he questions why this year is so important? At this point, physics is undergoing a revolution that will give rise to not just a new theory of gravity, but also will reveal the counter-intuitive and somewhat worrisome world of the very small. And a patent clerk in Bern, Switzerland , who will be at the centre of this revolution, is about to have a very good year.

The fifth year of the 20th Century will come to be referred to as Albert Einstein’s ‘ Annus mirabilis’ — or miracle year — and for good reason. The physicist will publish four papers in 1905, the first describing the photoelectric effect, the second detailing Brownian motion. But, as impressive those achievements are–one will see him awarded the Nobel after all–it’s the third and fourth papers we are interested in.

1905: young Albert Einstein contenplates the future, unaware he is about to change the way we think about time and space forever. (Original Author Unknown)

In these papers, Einstein will first introduce special relativity and then will describe mass-energy equivalence most famously represented by the reduced equation E=mc². It’s no exaggeration to say that these works will change how we think of reality entirely — especially from a physics standpoint.

Special relativity takes time — and whereas it had previously been believed to be its own separate entity — unites it with the four known dimensions of space. This creates a single fabric— spacetime. But the changes to the concept of time didn’t end there. Special relativity suggests that time is different depending on how one journeys through it. The faster an object moves the more time ‘dilates’ for that object. This idea of time running differently in different reference frames is how relativity gets its name. The most famous example for the time difference is the ‘twin paradox.’ Meet twin sisters Stella and Terra. Stella is about to undertake a mission to a distant star in a craft that is capable of travelling at near the speed of light, leaving her sister, Terra, behind on Earth.

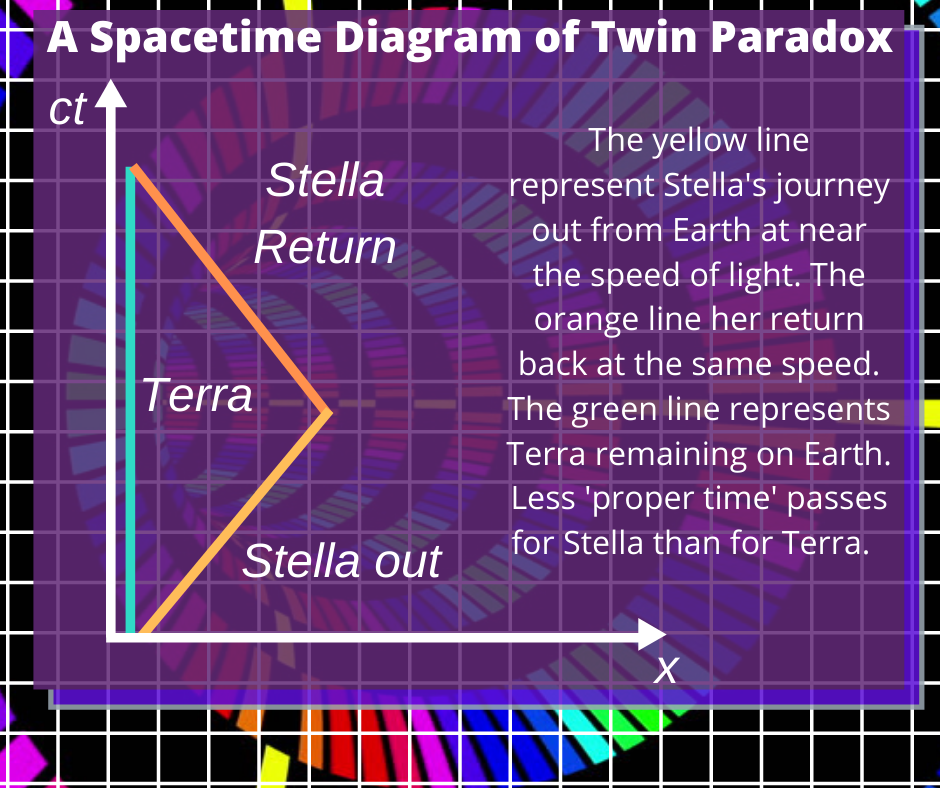
After travelling away from Earth at near the speed of light, then undertaking a return journey at a similar speed, Stella touches down and exits her craft to be greeter by Terra who has aged more in relation to herself. More time has passed for the ‘static’ Earthbound twin than for her sister who underwent the journey into space.

Thus, one could consider Stella to have travelled forward in time. How else could a pair of twins come to be of considerably different ages? That’s great, but what about moving backwards through time?

Well, if the faster a particle in a reference frame moves, the ‘slower’ time progresses in that frame, it raises the question, is there a speed at which time stands still? And if so, is there a speed beyond this at which time would move backwards?

Tachyons are hypothetical particles that travel faster than the speed of light — roughly considered as the speed at which time would stand still — and thus, would move backwards rather than forwards in time. The existence of tachyons would open up the possibility that our space-bound sister could receive a signal from Terra and send her back a tachyon response. Due to the nature of tachyons, this response could be received by Terra before she sent the initial signal.

Here’s where that becomes dangerous; what if Stella sends a tachyon signal back that says ‘Don’t signal me’? Then the original signal isn’t sent, leading to the question; what is Stella responding to?

Or in an even more extreme example; what if Stella sends a tachyon signal back that is intercepted by herself before she embarks on her journey, and that signal makes her decide not to embark on that journey in the first place? Then she’ll never be in space to send the tachyon signal… but, if that signal isn’t sent then she would have embarked on the journey…

And that’s the nature of the causality violating paradoxes that could arise from even the ability to send a signal back through time. Is there a way out of this paradox? Maybe…

Interlude. From the Journal of Albert Einstein

27th September 1905

A most astounding thing happened today. A young man in extraordinary attire visited me at the patent office. Introducing himself as ‘Marty’ the youngster proceeded to question me about my paper ‘On the Electrodynamics of Moving Bodies ‘– a surprise especially as it was only published yesterday.

In particular, the boy wanted to know about my theory’s implications on time travel! A pure flight of fancy of course… Unless… For another time perhaps.

If this wasn’t already unusual to the extreme, after our talk, I walked Marty to the banks of the Aare river where he told me that his transportation awaited him. I was, of course expecting a boat. I was therefore stunned when the boy stepped into a battered red box, which then simply disappeared.

I would say this was a figment of my overworked imagination, a result of tiredness arising from working the patent office during the day and writing papers at night. That is, were I the only witness!

A young man also saw the box vanish, and his shock must have been more extreme than mine for he stumbled into the river disappearing beneath its surface.

His body has not yet been recovered… I fear the worst.

Present Day: The Self Correcting Universe

As the battered old phone box rematerializes in the present day, Marty is determined to seek out an academic answer to the time travel paradox recounted to him in 1905.

He pays a visit to the University of Queensland where Bachelor of Advanced Science student Germain Tobar has been investigating the possibility of time travel. Under the supervision of physicist Dr Fabio Costa, Tobar believes that a mathematical ‘out’ from time travel paradoxes may be possible.

“Classical dynamics says if you know the state of a system at a particular time, this can tell us the entire history of the system,” Tobar explains. “For example, if I know the current position and velocity of an object falling under the force of gravity, I can calculate where it will be at any time.

“However, Einstein’s theory of general relativity predicts the existence of time loops or time travel — where an event can be both in the past and future of itself — theoretically turning the study of dynamics on its head.”

Tobar believes that the solution to time travel paradoxes is the fact that the Universe ‘corrects itself’ to remove the causality violation. Events will occur in such a way that paradoxes will be removed.

So, take our twin dilemma. As you recall Stella has sent herself a tachyon message that has persuaded her younger self not to head into space. Tobar’s theory — which he and his supervisor Costa say they arrived at mathematically by squaring the numbers involved in time travel calculations — suggests that one of two things could happen. Some event would force Stella to head into space, she could accidentally stumble into the capsule perhaps, or receive a better incentive to head out on her journey. Or another event could send out the tachyon signal, perhaps Stella could accidentally receive the signal from her replacement astronomer.

“No matter what you did, the salient events would just recalibrate around you,” says Tobar. “Try as you might, to create a paradox, the events will always adjust themselves, to avoid any inconsistency.

“The range of mathematical processes we discovered show that time travel with free will is logically possible in our universe without any paradox.”

Tobar’s solution is similar in many ways to he Novikov self-consistency principle — also known as Niven’s Law of the conservation of history — developed by Russian physicist Igor Dmitriyevich Novikov in the late 1970s. This theory suggested the use of geodesics similar to those used to describe the curvature of space in Einstein’s theory of general relativity to describe the curvature of time.

These closed time-like curves (CTCs) would prevent the violation of any causally linked events that lie on the same curve. It also suggests that time-travel would only be possible in areas where these CTCs exist, such as in the presence of wormholes as speculated by Kip Thorne and colleagues in the 1988 paper “Wormholes, Time Machines, and the Weak Energy Condition”. The events would cyclical and self-consistent.

The difference is, whereas Tobar suggests a self-correcting Universe, this idea strongly implies that time-travellers would not be able to change the past, whether this means they are physically prevented or whether they actually lack the ability to chose to do so. In our twin analogy, Stella’s replacement sends out a tachyon signal and travelling along a CTC, it knocks itself off course, meaning Stella receives rather than its intended target.

After listening to Tobar, strolling back to his time machine Marty takes a short cut through the local graveyard. Amongst the gravestones baring unfamiliar dates and names, he notices something worrying–chilling, in fact. There chiselled in ageing stone, his grandfather’s name. The date of his death reads 27th September 1905.

Interlude: From the Journal of Albert Einstein

29th September 1905

This morning the Emmenthaler Nachrichten reports that the body of the unfortunate young man who I witnessed fall into the Aare has been recovered. The paper even printed a picture of the young man.

I had not realised at the time, but the boy bares the most remarkable resemblance to Marty — the unusually dressed youngster who visited with me the very da y the boy fell…

Strange I such think of Marty’s attire so frequently, the young man told me his garish armless jacket, flannel shirt and ‘jeans’ were ‘all the rage in the ‘86.’

Yet, though I was seven in 1886 and have many vague memories from that year, I certainly do not remember such colourful clothes…

Lost in Time: How Quantum Physics provides an Escape Route From Time Travel Paradoxes

Marty folds the copy of the Emmenthaler Nachrichten up and places it on the floor of the cursed time machine that seems to have condemned him. The local paper has confirmed his worst fears; his trip to the past to visit Einstein doomed his grandfather.

After confirming his ancestry, he knows he is caught in a paradox. He waits to be wiped from time… After some time, Marty wonders how it could possibly be that he still lives? Quantum physics, or more specifically one interpretation of it has the answer. A way to escape the (literal) grandfather paradox.

The ‘many worlds’ interpretation of quantum mechanics was first suggested by Hugh Everett III in the 1950s as a solution to the problem of wave-function collapse demonstrated in Young’s infamous double-slit experiment.

As the electron is travelling it can be described as a wavefunction with a finite probability of passing through either slit S1 or slit S2. When the electron appears on the screen it isn’t smeared across it as a wave would be. It’s resolved as a particle-like point. We call this the collapse of the wavefunction as wave-like behaviour has disappeared, and it’s a key factor of the so-called Copenhagen interpretation of quantum mechanics. The question remained, why does the wavefunction collapse? Hugh Everett asked a different question; does the wavefunction collapse at all?

Everett imagined a situation in which instead of the wavefunction collapsing it continues to grow exponentially. So much so that eventually the entire universe is encompassed as just one of two possible states. A ‘world’ in which the particle passed through S1, and a world where the particle passed through S2. Everett also stated the same ‘splitting’ of states would occur for all quantum events, with different outcomes existing in different worlds in a superposition of states. The wavefunction simply looks like it has collapsed to us because we occupy one of these worlds. We are in a superposition of states and are forbidden from seeing the other outcome of the experiment. Marty realises that when he arrived back in 1905, a worldline split occurred. He is no longer in the world he came from– which he labels World 1. Instead, he has created and occupies a new world. When he travels forward in time to speak to Tobar he travels along the timeline of this world–World 2. This makes total sense. In the world Marty left, a phone box never appeared on the banks of the Aera on September 27th 1905. This world is intrinsically different than the one he left.

He never existed in this world and in truth he hasn’t actually killed his grandfather. His grandfather exists safe and sound back in 1905 of World 1. If the Many World’s Interpretation of quantum physics is the correct solution to the grandfather paradox, however, then Marty can never return to World 1. It’s intrinsic to this interpretation that superpositioned worlds cannot interact with each other.

With reference to the diagrams above, Marty can only move ‘left and down’ or ‘right’–up is a forbidden direction because it’s his presence at a particular moment that creates the new world. This makes total sense, he has changed history and is in a world in which he appeared in 1905. He can’t change that fact. The non-interaction rule means no matter what measures he takes, every time he travels back into the past he creates a new state and hops ‘down’ to that state and can then only move forward in time (right) on that line.

So what happens when Marty travels back to the past in an attempt to rescue his world? He inadvertently creates another state–World 3. This world may resemble World 1 & 2 in almost every conceivable way, but according to the application of the interpretation, it is not the same due to one event–one extra phone box on the banks of the River Aare for each journey back.

As Marty continues to attempt to get back to World 1 — his home — he realises he now lives in a world in which one day in September 1905 on the streets of Bern, hundreds of phone box suddenly appeared on the banks of the Aare, and then simply disappeared.

He also realises that his predicament answers the question ‘if time travellers exist why do they never appear in our time?’ The truth being, that if a person exists in the world from which these travellers departed they can never ‘get back’ to this primary timeline.

To someone in World 1, the advent of time travel will just result in the gradual disappearance of daring physicists. That’s the moment it dawns on Marty that as far as World 1 — his world — is concerned, he stepped in a phone box one day and vanished, never to return. Marty escaped the time travel paradox but doomed himself to wander alternate worlds. Hey… how do we get our time machine back?

Was this helpful?

U.S. issues travel warning for Israel with Iran attack believed to be imminent and fear Gaza war could spread

By Debora Patta , Tucker Reals

Updated on: April 13, 2024 / 5:25 PM EDT / CBS News

Update: Iran launched drone attacks against Israel on Saturday. Read CBS News' latest coverage here .

Tel Aviv — Israel is bracing for a worst-case scenario that U.S. officials believe could materialize within just hours — the possibility of a direct attack on Israeli soil by Iran in retaliation for a strike almost two weeks ago that killed seven Iranian military officers. Iran has vowed to take revenge for Israel killing its commanders, who were hit by an April 1 strike on the Iranian embassy in Syria's capital.

Two U.S. officials told CBS News that a major Iranian attack against Israel was expected as soon as Friday, possibly to include more than 100 drones and dozens of missiles aimed at military targets inside the country. Sources have told CBS News the retaliation could include attacks carried out both by Iranian forces, and proxy groups around the region that it has been funneling additional arms to for weeks.

The officials said it would be challenging for the Israelis to defend against an attack of that magnitude, and while they held out the possibility that the Iranians could opt for a smaller-scale attack to avoid a dramatic escalation, their retaliation was believed to be imminent.

Asked Friday how imminent he believes an attack is, President Biden responded, "I don't want to get into secure information, but my expectation is sooner than later." The president urged Iran not to move forward, saying his message to Tehran was: "Don't."

Tehran has not indicated publicly how or when it will return fire, so it's unclear how far Iran's leaders will go. If they decide to carry out a direct attack on Israel, there's fear it could blow Israel's ongoing war against Iranian ally Hamas up into a much wider regional conflict.

With the Iranian retaliation expected at any time, the U.S. State Department on Thursday warned Americans in Israel not to travel outside major cities, which are better protected from incoming rocket fire by the country's Iron Dome missile defense system. The latest guidance noted that travel by U.S. government employees in Israel could be further restricted with little notice as things develop in the tinderbox region.

"Whoever harms us, we will harm them," Prime Minister Benjamin Netanyahu vowed Thursday as he visited troops at an Israel Defense Forces airbase. "We are prepared … both defensively and offensively."

Iran-Burning Flags Of The U.S. And Israel

On Saturday, all U.S. embassies in the Middle East were put on high alert and required to hold emergency action committee meetings. Diplomats in Lebanon and Israel were specifically told not to travel to certain areas within those countries.

Sima Shine, a security expert and former official with Israel's national intelligence agency Mossad, told CBS News it was a dangerous moment for the region, and the "most worried" she has been. She said anxiety over an all-out war was likely just as high "on both sides, in Israel and in Iran."

If Iran does choose to strike Israel directly, it could involve a complex missile and drone attack similar to the one Iranian forces launched against a Saudi oil facility in 2019 .

"They will try to do it on the military or some military asset," Shine predicted. "But the question will be the damage. If there would be many injured people, killed or injured … I think it has the potential for a huge escalation."

Iran- International Jerusalem Day Rally In Tehran

Shine stressed, however, that she still believes neither side actually wants a regional conflict.

U.S. "really trying to avoid war"

The U.S. sent a senior general to Israel this week to coordinate with the close American ally on any response it might make to an Iranian attack. Speaking Friday on "CBS Mornings," America's top military officer said, "we're really trying to avoid war."

"This is part of the dialogue that I have with my counterparts within the region, to include the Israeli chief of defense, who I talked to yesterday," said Joint Chiefs chairman Gen. Charles Q. Brown, Jr., adding that the U.S. military was "doing things not only to prevent a war, but at the same time, one of my primary things is to make sure all the forces in the region are protected."

"My role, as the chairman of the Joint Chiefs, is to plan and prepare," Brown said. "That's one thing we do very well."

Brown's Israeli counterpart, Chief of the General Staff Lt. Gen. Herzi Halevi, "completed a comprehensive situational assessment on the readiness of the IDF for all scenarios," Israel's military said Friday.

"The IDF is very strongly prepared, both offensively and defensively, against any threat," Halevi was quoted as saying in the statement. "The IDF continues to monitor closely what is happening in Iran and different arenas, constantly preparing to deal with existing and potential threats in coordination with the United States Armed Forces."

The IDF said the visiting U.S. general, Central Command chief Gen. Michael Erik Kurilla, was taking part in the IDF's situational assessment.

The dilemma for Iran, said Israeli expert Shine, is to figure out how to deliver its promised response to Israel's attack in Syria, but in a way that does not lead to further escalation. Likewise, Shine said Israel could choose to show restraint when it responds to whatever Iran eventually does.

If either side gets the balance wrong, the consequences for the region, and even the world, could be dire.

Weijia Jiang, David Martin, Margaret Brennan and Olivia Gazis contributed reporting.

Middle East
Benjamin Netanyahu

Debora Patta is a CBS News foreign correspondent based in Johannesburg. Since joining CBS News in 2013, she has reported on major stories across Africa, the Middle East and Europe. Edward R. Murrow and Scripps Howard awards are among the many accolades Patta has received for her work.

More from CBS News

What Iran attacked Israel with, and what actually made it through

Israel blames starvation in Gaza on U.N. making excuses

Trump allies encourage visits with foreign leaders at Mar-a-Lago before election

Johnson faces growing pressure over Ukraine, Israel aid

IMAGES

[THEORY] Time Travel Metaphysics/Paradoxes Infographic : timetravel
Three Amazing Time Travel Paradoxes
Time Travel Paradoxes (Animated Infographic)
What Are Some Famous Time Paradoxes?
Time Travel Paradoxes : What Are They?
The paradoxes of time travel

VIDEO

Time Travel Incredible Theories and Paradoxes
Paradoxes of Time Travel
How to Train a Bayesian Brain?
Cracking the Immortality Paradox: Journey into Time Travel
Time Travel into the past! explained
The Science of Time Travel: Preventing Paradoxes Explained

COMMENTS

5 Bizarre Paradoxes Of Time Travel Explained
1: Predestination Paradox. A Predestination Paradox occurs when the actions of a person traveling back in time become part of past events, and may ultimately cause the event he is trying to prevent to take place. The result is a 'temporal causality loop' in which Event 1 in the past influences Event 2 in the future (time travel to the past ...
Temporal paradox
A temporal paradox, time paradox, or time travel paradox, is a paradox, an apparent contradiction, or logical contradiction associated with the idea of time travel or other foreknowledge of the future. While the notion of time travel to the future complies with the current understanding of physics via relativistic time dilation, temporal paradoxes arise from circumstances involving ...
Time travel could be possible, but only with parallel timelines
The other main issue is less practical, but more significant: it is the observation that time travel seems to contradict logic, in the form of time travel paradoxes. There are several types of ...
Can we time travel? A theoretical physicist provides some answers
There is also the matter of time-travel paradoxes; we can — hypothetically — resolve these if free will is an illusion, if many worlds exist or if the past can only be witnessed but not ...
Is time travel even possible? An astrophysicist explains the science
There are also paradoxes associated with time travel. The famous " grandfather paradox " is a hypothetical problem that could arise if someone traveled back in time and accidentally prevented ...
Time Travel Paradoxes
Time Travel Paradoxes - Time travel problems include the grandfather paradox and parallel universes. Learn about some if the different kinds of time travel problems. ... But then there's another possibility: The quantum theory that the future or past you travel into might just be a parallel universe. Think of it as a separate sandbox: You can ...
The Physics of Time Travel: Examining the Possibilities and Paradoxes
The Paradoxes of Time Travel. There are a number of paradoxes that would need to be resolved before time travel could become a reality. Some of the most famous time travel paradoxes include:
The Time-Travel Paradoxes
The Time-Travel Paradoxes. Rami Shalheveth, David Madar. March 22, 2020. 12 min. Science Panorama. ... push the button, and go from time A to time B, through all the times in between. But there's a catch, if we are only travelling through time, then to the casual observer, the time machine continuously exists in the same space between the ...
Temporal Paradoxes
Chapter 2 surveys the various theories of time and explores their consequences for the possibility of time travel. Section 1 introduces the tradi. ... Ryan, 'Temporal Paradoxes', Paradoxes of Time Travel (Oxford, 2017; online edn ... Of course, there are many different things one might mean by "reducible," but it is natural to ...
Time Travel and Modern Physics
First published Thu Feb 17, 2000; substantive revision Mon Mar 6, 2023. Time travel has been a staple of science fiction. With the advent of general relativity it has been entertained by serious physicists. But, especially in the philosophy literature, there have been arguments that time travel is inherently paradoxical.
PDF Can we time travel? A theoretical physicist provides some answers
There is also the matter of time-travel paradoxes; we can—hypothetically—resolve these if free will is an illusion, if many worlds exist or if the past can only be witnessed but not experienced.
Paradoxes of Time Travel
Abstract. Paradoxes of Time Travel is a comprehensive study of the philosophical issues raised by the possibility of time travel. The book begins, in Chapter 1, by explaining the concept of time travel and clarifying the central question to be addressed: Is time travel compatible with the laws of metaphysics and, in particular, the laws ...
Two Scientifically Plausible Conceptions of Time Travel and Their
The many-worlds theory of time travel not only renders this story plausible but also, as Gott observes, it suggests that among the many universes that would consequently exist, there is one that ...
Paradoxes of Time Travel
Ryan Wasserman, Paradoxes of Time Travel, Oxford University Press, 2018, 240pp., $60.00, ISBN 9780198793335. Reviewed by . John W. Carroll, North Carolina State. 2018.05.11. ... There are metaphysics books on time that give some attention to time travel, but, as far as I know, this is the first book length work devoted to the topic of time ...
How many types of paradoxes are there in time travel and what ...
There are a lot of paradoxes associated with time travel but my favourite is the predestination paradox in which a person goes back in the past and gets involved in an event to alter the future but instead, that results in that event being fulfilled and you were the soul reason for this endless cycle.
Time Travel: Problems, Paradoxes, and Practicalities
Jan 10, 2024. Photo by Sachin Khadka on Unsplash. Time travel is a common trope in fiction. It refers to the act of being able to travel backwards or forwards in time to witness events that have ...
Time travel paradoxes and multiple histories
If time travel is possible, it seems to inevitably lead to paradoxes. These include consistency paradoxes, such as the famous grandfather paradox, and bootstrap paradoxes, where something is created out of nothing. One proposed class of resolutions to these paradoxes allows for multiple histories (or timelines) such that any changes to the past occur in a new history, independent of the one ...
Time Travel Could Be Possible, But Only With Parallel Timelines
Since I cannot destroy the time machine in the original timeline, which is the one I actually used to travel back in time, there is no paradox. After working on time travel paradoxes for the last three years , I have become increasingly convinced that time travel could be possible, but only if our universe can allow multiple histories to coexist.
There's One Way Time Travel Could Be Possible, According to This
Eliminating the paradoxes. There's a common misconception in science fiction that paradoxes can be "created." Time travellers are usually warned not to make significant changes to the past and to avoid meeting their past selves for this exact reason. Examples of this may be found in many time travel movies, such as the Back to the Future trilogy.
How Does Multiverse Theory Relate to Time Travel?
The theoretical physics and paradoxes of time travel often brush up against multiverse theory and the idea of alternate universes. ... (extremely hypothetical) view, there are many universes out there that contain alternate realities from the one you know. There's one where your grandfather died. There's another where no stars ever formed ...
The Grandfather Paradox: Is Time Travel Possible?
The Grandfather Paradox Explained: The Grandfather Paradox is a classic paradoxical scenario that arises from the notion of time travel. It posits a hypothetical situation in which a person ...
List of paradoxes
Birthday paradox: In a random group of only 23 people, there is a better than 50/50 chance two of them have the same birthday. Borel's paradox: Conditional probability density functions are not invariant under coordinate transformations. Boy or Girl paradox: A two-child family has at least one boy.
Time Travel Without the Paradoxes
Lost in Time: How Quantum Physics provides an Escape Route From Time Travel Paradoxes Marty folds the copy of the Emmenthaler Nachrichten up and places it on the floor of the cursed time machine ...
U.S. issues travel warning for Israel with Iran attack believed to be
With the Iranian retaliation expected at any time, the U.S. State Department on Thursday warned Americans in Israel not to travel outside major cities, which are better protected from incoming ...
A year's worth of rain plunges normally dry Dubai underwater
Nearly 4 inches (100 mm) of rain fell over the course of just 12 hours on Tuesday, according to weather observations at the airport - around what Dubai usually records in an entire year ...

5 Bizarre Paradoxes Of Time Travel Explained

Types of Temporal Paradoxes

1: Predestination Paradox

– Cinema Treatment

2: Bootstrap Paradox

3: Grandfather Paradox

4: Let’s Kill Hitler Paradox

5: Polchinski’s Paradox

Are Self-Fulfilling Prophecies Paradoxes?

Are Time Paradoxes Inevitable?

Related Posts

Is time travel even possible? An astrophysicist explains the science behind the science fiction

Disclosure statement

Time is relative

Paradoxes and failed dinner parties

Telescopes are time machines

Deputy Social Media Producer

Research Fellow /Senior Research Fellow – Implementation Science

Associate Professor, Occupational Therapy

GRAINS RESEARCH AND DEVELOPMENT CORPORATION CHAIRPERSON

Faculty of Law - Academic Appointment Opportunities

How Time Travel Works

Time Travel Paradoxes

Related Articles

More Great Links

The Time-Travel Paradoxes

The Grandfather Paradox

The Time Loop

Time travelers – where have all they gone?

One way or round trip?

Advanced time travel

How to travel in time and stay alive

Time Travelling Grammar

Bibliography

Time Travel and Modern Physics

1. Paradoxes Lost?

Support SEP

Paradoxes of Time Travel

Signed in as

Personal account

Institutional access

IP based access

Sign in through your institution

Sign in with a library card

Society Members

Sign in through society site

Sign in using a personal account

Viewing your signed in accounts

Signed in but can't access content

This Feature Is Available To Subscribers Only

Paradoxes of Time Travel

How Does Multiverse Theory Relate to Time Travel?

Is It Possible To Travel Back in Time?

The Trouble With Changing the Past

The Grandfather Paradox

Are There Multiple Universes?

Splitting-Off Worlds in Quantum Mechanics

No Travel Between Worlds in Quantum Mechanics

Bubble Universe Theory

Time Still Marches Forward in the Multiverse

The Grandfather Paradox: Is Time Travel Possible?

Time Travel Without the Paradoxes

A Trip to 1905: Einstein’s Spacetime is Born

Interlude. From the Journal of Albert Einstein

Present Day: The Self Correcting Universe

Interlude: From the Journal of Albert Einstein

Lost in Time: How Quantum Physics provides an Escape Route From Time Travel Paradoxes

Was this helpful?

U.S. issues travel warning for Israel with Iran attack believed to be imminent and fear Gaza war could spread

U.S. "really trying to avoid war"

More from CBS News

What Iran attacked Israel with, and what actually made it through

Israel blames starvation in Gaza on U.N. making excuses

Trump allies encourage visits with foreign leaders at Mar-a-Lago before election

Johnson faces growing pressure over Ukraine, Israel aid

IMAGES

VIDEO

COMMENTS