travelling salesman problem visualization

Traveling Salesman Problem

The traveling salesman problem (TSP) asks the question, "Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city and returns to the origin city?".

This project

• The goal of this site is to be an educational resource to help visualize, learn, and develop different algorithms for the traveling salesman problem in a way that's easily accessible
• As you apply different algorithms, the current best path is saved and used as input to whatever you run next. (e.g. shortest path first -> branch and bound). The order in which you apply different algorithms to the problem is sometimes referred to the meta-heuristic strategy.

Heuristic algorithms

Heuristic algorithms attempt to find a good approximation of the optimal path within a more reasonable amount of time.

Construction - Build a path (e.g. shortest path)

• Shortest Path

Arbitrary Insertion

Furthest insertion.

• Nearest Insertion
• Convex Hull Insertion*
• Simulated Annealing*

Improvement - Attempt to take an existing constructed path and improve on it

• 2-Opt Inversion
• 2-Opt Reciprcal Exchange*

Exhaustive algorithms

Exhaustive algorithms will always find the best possible solution by evaluating every possible path. These algorithms are typically significantly more expensive then the heuristic algorithms discussed next. The exhaustive algorithms implemented so far include:

• Random Paths

Depth First Search (Brute Force)

• Branch and Bound (Cost)
• Branch and Bound (Cost, Intersections)*

Dependencies

These are the main tools used to build this site:

• web workers
• material-ui

Contributing

Pull requests are always welcome! Also, feel free to raise any ideas, suggestions, or bugs as an issue.

This is an exhaustive, brute-force algorithm. It is guaranteed to find the best possible path, however depending on the number of points in the traveling salesman problem it is likely impractical. For example,

• With 10 points there are 181,400 paths to evaluate.
• With 11 points, there are 1,814,000.
• With 12 points there are 19,960,000.
• With 20 points there are 60,820,000,000,000,000, give or take.
• With 25 points there are 310,200,000,000,000,000,000,000, give or take.

This is factorial growth, and it quickly makes the TSP impractical to brute force. That is why heuristics exist to give a good approximation of the best path, but it is very difficult to determine without a doubt what the best path is for a reasonably sized traveling salesman problem.

This is a recursive, depth-first-search algorithm, as follows:

• From the starting point
• For all other points not visited
• If there are no points left return the current cost/path
• Else, go to every remaining point and
• Mark that point as visited
• " recurse " through those paths (go back to 1. )

Implementation

Nearest neighbor.

This is a heuristic, greedy algorithm also known as nearest neighbor. It continually chooses the best looking option from the current state.

• sort the remaining available points based on cost (distance)
• Choose the closest point and go there
• Chosen point is no longer an "available point"
• Continue this way until there are no available points, and then return to the start.

Two-Opt inversion

This algorithm is also known as 2-opt, 2-opt mutation, and cross-aversion. The general goal is to find places where the path crosses over itself, and then "undo" that crossing. It repeats until there are no crossings. A characteristic of this algorithm is that afterwards the path is guaranteed to have no crossings.

• While a better path has not been found.
• For each pair of points:
• Reverse the path between the selected points.
• If the new path is cheaper (shorter), keep it and continue searching. Remember that we found a better path.
• If not, revert the path and continue searching.

This is a heuristic construction algorithm. It select a random point, and then figures out where the best place to put it will be.

• First, go to the closest point
• Choose a random point to go to
• Find the cheapest place to add it in the path
• Continue from #3 until there are no available points, and then return to the start.

This is an impractical, albeit exhaustive algorithm. It is here only for demonstration purposes, but will not find a reasonable path for traveling salesman problems above 7 or 8 points.

I consider it exhaustive because if it runs for infinity, eventually it will encounter every possible path.

• From the starting path
• Randomly shuffle the path
• If it's better, keep it
• If not, ditch it and keep going

Two-Opt Reciprocal Exchange

This algorithm is similar to the 2-opt mutation or inversion algorithm, although generally will find a less optimal path. However, the computational cost of calculating new solutions is less intensive.

The big difference with 2-opt mutation is not reversing the path between the 2 points. This algorithm is not always going to find a path that doesn't cross itself.

It could be worthwhile to try this algorithm prior to 2-opt inversion because of the cheaper cost of calculation, but probably not.

• Swap the points in the path. That is, go to point B before point A, continue along the same path, and go to point A where point B was.

Branch and Bound on Cost

This is a recursive algorithm, similar to depth first search, that is guaranteed to find the optimal solution.

The candidate solution space is generated by systematically traversing possible paths, and discarding large subsets of fruitless candidates by comparing the current solution to an upper and lower bound. In this case, the upper bound is the best path found so far.

While evaluating paths, if at any point the current solution is already more expensive (longer) than the best complete path discovered, there is no point continuing.

For example, imagine:

• A -> B -> C -> D -> E -> A was already found with a cost of 100.
• We are evaluating A -> C -> E, which has a cost of 110. There is no point evaluating the remaining solutions.

Instead of continuing to evaluate all of the child solutions from here, we can go down a different path, eliminating candidates not worth evaluating:

• A -> C -> E -> D -> B -> A
• A -> C -> E -> B -> D -> A

Implementation is very similar to depth first search, with the exception that we cut paths that are already longer than the current best.

This is a heuristic construction algorithm. It selects the closest point to the path, and then figures out where the best place to put it will be.

• Choose the point that is nearest to the current path

Branch and Bound (Cost, Intersections)

This is the same as branch and bound on cost, with an additional heuristic added to further minimize the search space.

While traversing paths, if at any point the path intersects (crosses over) itself, than backtrack and try the next way. It's been proven that an optimal path will never contain crossings.

Implementation is almost identical to branch and bound on cost only, with the added heuristic below:

This is a heuristic construction algorithm. It selects the furthest point from the path, and then figures out where the best place to put it will be.

• Choose the point that is furthest from any of the points on the path

Convex Hull

This is a heuristic construction algorithm. It starts by building the convex hull , and adding interior points from there. This implmentation uses another heuristic for insertion based on the ratio of the cost of adding the new point to the overall length of the segment, however any insertion algorithm could be applied after building the hull.

There are a number of algorithms to determine the convex hull. This implementation uses the gift wrapping algorithm .

In essence, the steps are:

• Determine the leftmost point
• Continually add the most counterclockwise point until the convex hull is formed
• For each remaining point p, find the segment i => j in the hull that minimizes cost(i -> p) + cost(p -> j) - cost(i -> j)
• Of those, choose p that minimizes cost(i -> p -> j) / cost(i -> j)
• Add p to the path between i and j
• Repeat from #3 until there are no remaining points

Simulated Annealing

Simulated annealing (SA) is a probabilistic technique for approximating the global optimum of a given function. Specifically, it is a metaheuristic to approximate global optimization in a large search space for an optimization problem.

For problems where finding an approximate global optimum is more important than finding a precise local optimum in a fixed amount of time, simulated annealing may be preferable to exact algorithms

Visualize algorithms for the traveling salesman problem. Use the controls below to plot points, choose an algorithm, and control execution. (Hint: try a construction alogorithm followed by an improvement algorithm)

Travelling Salesman

Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city exactly once and returns to the origin city?

Touch the canvas in order to add a point. You cannot add points when solution is being calculated.

• Nearest Neighbour: Start at a particular node. Travel to the nearest node. Repeat. This algorithm is very simple to implement.
• Greedy Heuristic: Form the initial path with shorter edges, and connect them.
• Simulated Annealing: Inspired by the way crystals cool, this method tries to converge to a local minima while implementing a cooling schedule. In every step, two nodes from the path are switched, and the resulting path is accepted or rejected using Metropolis algorithm (please find intricate details here ).
• Genetic Algorithm: A poplation of entities whose genes comprise of paths, and whose fitness is based on how short the paths are. Fitter entities have greater chance of their genes making it into the offspring. Also uses mutation (to explore prospectively better avenues) and recombination (to combine the best of two genes).
• Ant Colony Optimization: Initially, a population of ants randomly traverse the graph. By gauging the shortness of each edge, they leave more pheromones along that edge. In the next iteration, at every node, the ants choose the edge on a probabilistic manner, weighted by pheromone strength. Both, genetic algorithm and ant colony optimization are called metaheuristic methods because they solve the problem at hand by working at a higher level, instead of directly tackling the problem.
• Christofides' Algorithm Considered the gold standard of solving the Travelling Salesman Problem, this algorithm utilizes insights from an easily solvable problem in graph theory (constructing a minimal spanning tree from a given graph) and manipulates it to arrive at (on average) comparatively shorter paths.
• I will try to make simulations of the optimized algorithms above, if time permits.
• When there are 8+ points, then an initial lag is expected before the solving process starts
• With 10 points, an average time of 49 minutes was required to find the solution to the route
• Simulation may lag on lower-end computers and phones
• Related: Ant Colony Optimization

Developed by ChanRT | Fork me at GitHub

• ENGINEERING
• What's the point?
• life cycles
• engineering
• data visualization
• biogeochemistry
• social science
• computer science
• epidemiology

11 Animated Algorithms for the Traveling Salesman Problem

For the visual learners, here’s an animated collection of some well-known heuristics and algorithms in action.

TSP Algorithms and heuristics

Although we haven’t been able to quickly find optimal solutions to NP problems like the Traveling Salesman Problem, "good-enough" solutions to NP problems can be quickly found [1] .

For the visual learners, here’s an animated collection of some well-known heuristics and algorithms in action. Researchers often use these methods as sub-routines for their own algorithms and heuristics. This is not an exhaustive list.

For ease of visual comparison we use Dantzig49 as the common TSP problem, in Euclidean space. Dantzig49 has 49 cities — one city in each contiguous US State, plus Washington DC.

1: Greedy Algorithm

A greedy algorithm is a general term for algorithms that try to add the lowest cost possible in each iteration, even if they result in sub-optimal combinations.

In this example, all possible edges are sorted by distance, shortest to longest. Then the shortest edge that will neither create a vertex with more than 2 edges, nor a cycle with less than the total number of cities is added. This is repeated until we have a cycle containing all of the cities.

Although all the heuristics here cannot guarantee an optimal solution, greedy algorithms are known to be especially sub-optimal for the TSP.

2: Nearest Neighbor

The nearest neighbor heuristic is another greedy algorithm, or what some may call naive. It starts at one city and connects with the closest unvisited city. It repeats until every city has been visited. It then returns to the starting city.

Karl Menger, who first defined the TSP, noted that nearest neighbor is a sub-optimal method:

"The rule that one first should go from the staring point to the closest point, then to the point closest to this, etc., in general does not yield the shortest route."

The time complexity of the nearest neighbor algorithm is O(n^2) . The number of computations required will not grow faster than n^2.

3: Nearest Insertion

Insertion algorithms add new points between existing points on a tour as it grows.

One implementation of Nearest Insertion begins with two cities. It then repeatedly finds the city not already in the tour that is closest to any city in the tour, and places it between whichever two cities would cause the resulting tour to be the shortest possible. It stops when no more insertions remain.

The nearest insertion algorithm is O(n^2)

4: Cheapest Insertion

Like Nearest Insertion, Cheapest Insertion also begins with two cities. It then finds the city not already in the tour that when placed between two connected cities in the subtour will result in the shortest possible tour. It inserts the city between the two connected cities, and repeats until there are no more insertions left.

The cheapest insertion algorithm is O(n^2 log2(n))

5: Random Insertion

Random Insertion also begins with two cities. It then randomly selects a city not already in the tour and inserts it between two cities in the tour. Rinse, wash, repeat.

Time complexity: O(n^2)

6: Farthest Insertion

Unlike the other insertions, Farthest Insertion begins with a city and connects it with the city that is furthest from it.

It then repeatedly finds the city not already in the tour that is furthest from any city in the tour, and places it between whichever two cities would cause the resulting tour to be the shortest possible.

7: Christofides Algorithm

Christofides algorithm is a heuristic with a 3/2 approximation guarantee. In the worst case the tour is no longer than 3/2 the length of the optimum tour.

Due to its speed and 3/2 approximation guarantee, Christofides algorithm is often used to construct an upper bound, as an initial tour which will be further optimized using tour improvement heuristics, or as an upper bound to help limit the search space for branch and cut techniques used in search of the optimal route.

For it to work, it requires distances between cities to be symmetric and obey the triangle inequality, which is what you'll find in a typical x,y coordinate plane (metric space). Published in 1976, it continues to hold the record for the best approximation ratio for metric space.

The algorithm is intricate [2] . Its time complexity is O(n^4)

A problem is called k-Optimal if we cannot improve the tour by switching k edges.

Each k-Opt iteration takes O(n^k) time.

2-Opt is a local search tour improvement algorithm proposed by Croes in 1958 [3] . It originates from the idea that tours with edges that cross over aren’t optimal. 2-opt will consider every possible 2-edge swap, swapping 2 edges when it results in an improved tour.

2-opt takes O(n^2) time per iteration.

3-opt is a generalization of 2-opt, where 3 edges are swapped at a time. When 3 edges are removed, there are 7 different ways of reconnecting them, so they're all considered.

The time complexity of 3-opt is O(n^3) for every 3-opt iteration.

10: Lin-Kernighan Heuristic

Lin-Kernighan is an optimized k-Opt tour-improvement heuristic. It takes a tour and tries to improve it.

By allowing some of the intermediate tours to be more costly than the initial tour, Lin-Kernighan can go well beyond the point where a simple 2-Opt would terminate [4] .

Implementations of the Lin-Kernighan heuristic such as Keld Helsgaun's LKH may use "walk" sequences of 2-Opt, 3-Opt, 4-Opt, 5-Opt, “kicks” to escape local minima, sensitivity analysis to direct and restrict the search, as well as other methods.

LKH has 2 versions; the original and LKH-2 released later. Although it's a heuristic and not an exact algorithm, it frequently produces optimal solutions. It has converged upon the optimum route of every tour with a known optimum length. At one point in time or another it has also set records for every problem with unknown optimums, such as the World TSP, which has 1,900,000 locations.

11: Chained Lin-Kernighan

Chained Lin-Kernighan is a tour improvement method built on top of the Lin-Kernighan heuristic:

Lawrence Weru

Larry is a TEDx speaker, Harvard Medical School Dean's Scholar, Florida State University "Notable Nole," and has served as an invited speaker at Harvard, FSU, and USF. Larry's contributions are featured by Harvard University, Fast Company, and Gizmodo Japan, and cited in books by Routledge and No Starch Press. His stories and opinions are published in Slate, Vox, Toronto Star, Orlando Sentinel, and Vancouver Sun, among others. He illustrates the sciences for a more just and sustainable world.

You might also like

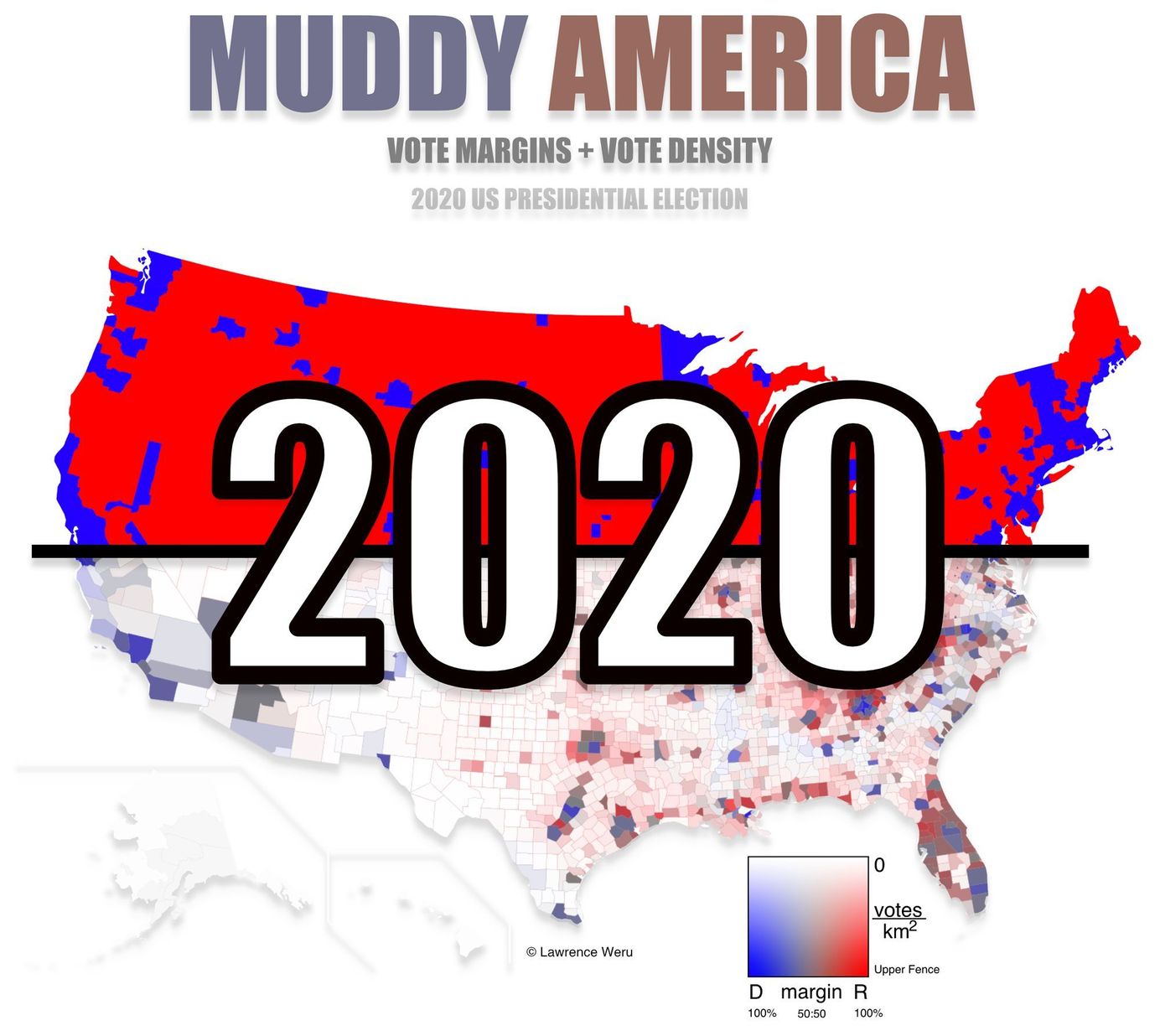
2020 Presidential Election County Level Muddy Map Paid Members Public

2020 US Presidential Election Interactive County-Level Vote Map

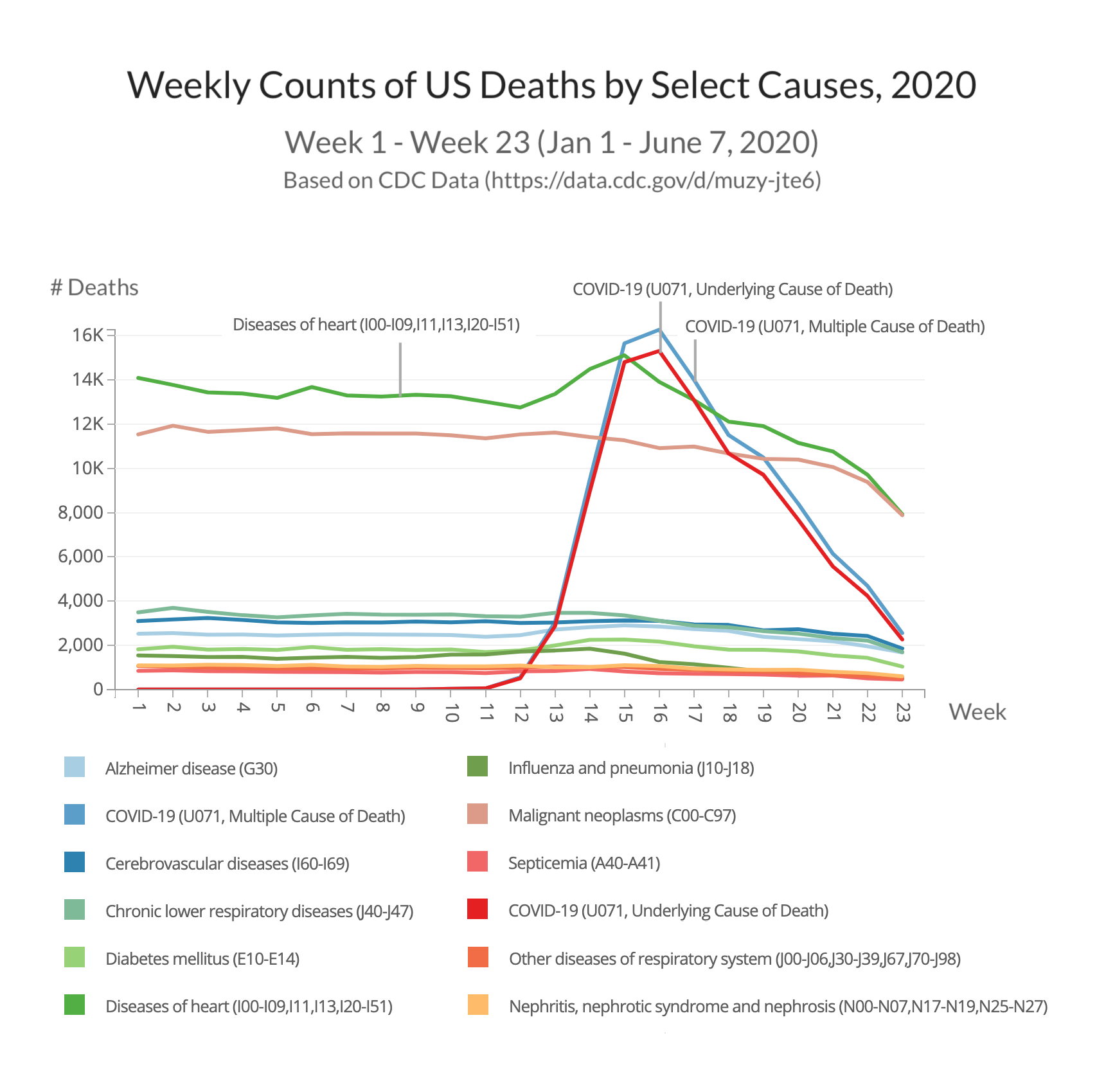
Weekly Counts of US Deaths by Select Causes through June 2020 Paid Members Public

This graph uses CDC data to compare COVID deaths with other causes of deaths.

STEM Lounge Newsletter

Be the first to receive the latest updates in your inbox.

Featured Posts

Tokyo olympics college medal count 🏅.

Muddy America : Color Balancing The US Election Map - Infographic

The trouble with the purple election map.

This website uses cookies to ensure you get the best experience on our website. You may opt out by using any cookie-blocking technology, such as your browser add-on of choice. Got it!

• This website needs Javascript in order to be displayed properly.
• Javascript is currently deactivated in your browser. A manual for the activation of Javascript can be found here .

• Introduction
• Create game
• Optimal tour
• Description of the algorithm
• Calculation steps

Shortest round trips

Welcome to the tsp game.

This website is about the so-called "Traveling Salesman Problem".

It deals with the question, how to plan a complete round trip through a certain number of cities to obtain the shortest tour possible. This question can be answered quite easily for four cities. However, it gets complicated when the number of cities is increased. There exist for example 181.440 different tours through just ten cities.

How can one find the shortest tour on twenty or even more cities?

For this reason, various algorithms have been invented, which try to solve the Traveling Salesman Problem as fast as possible.

And now it is your turn!

Create a new game in the next tab and try to find a shortest tour yourself! Afterwards, you may have a look at the solution and the calculation steps of the applied algorithms.

What would you like to do first?

Repeat game

On this page you can create a new game, find your tour, see the solution, repeat the current game, test your logistic skills and draw the shortest round trip you can find..

Do not forget to visit every city exactly once!

By changing the tab, the drawing mode will be terminated.

There is no way back to the "Play game" tab.

Congratulations! Your tour is optimal.

Too bad unfortunately, your tour is not optimal., too bad unfortunately, your tour does not visit all nodes., too bad unfortunately, your tour contains subtours., how has the solution been calculated.

In this tab you may have a look at the optimal tour and the corresponding calculation steps.

In the Description of the algorithm you may find more details on the applied algorithms of the different steps.

Graphs and algorithms

• 'Heuristics', which find a round trip, but do not indicate its optimality in relation to an optimal solution. Its length is always larger than the length of an optimal tour. It is than called 'upper bound'.
• "Exact solver", which converge to an optimal round trip slowly. Found paths are never longer than an optimal solution. Therefore, their length is called 'lower bound'. Their result is rarely a round trip through all nodes.

Nearest neighbour algorithm

Multiple fragment algorithm.

• There are no more than two incident edges allowed for each node.
• No circles are allowed.

Lagrangian relaxation

• Remove one node from the graph.
• Add edges between the remaining nodes in ascending order, like in the Multiple Fragment algorithm. There may be more than two edges incident to one node. However, circles are not allowed.
• Now add the removed node together with its two shortest incident edges to the graph. If a round trip is obtained, stop. There is no shorter round trip. Otherwise, one continues as follows.
• The aim is to have exactly two edges incident to one node. Therefore, find out by which number the number of incident edges differs from 2. Say four edges are incident to a node, then the result is 2. One incident edge leads to -1. Add the result to the length of all incident edges.
• Return to the first step.

Branch and Bound

• e and f are forced edges. All other edges are permitted.
• e is forced and f permitted. Edges that have been free before this step will stay free.
• e is permitted. All other edges stay free, if they have been before.

Origins of the Traveling Salesman Problem

The application, studying mathematics at the tum, a last remark about this page's goal and citations.

Chair M9 of Technische Universität München does research in the fields of discrete mathematics, applied geometry and the optimization of mathematical problems. The problem and corresponding algorithms presented here are a famous example for the application of mathematics on an applied problem (and can be assigned to the field of combinatorial optimization). This page shall help the reader to recognize the application of mathematics to real life problems and to understand easy mathematical solution methods used. The algorithms presented were chosen according to understandability, they do not represent fields of research of the chair.

To cite this page, please use the following information:

There is no solution available.

The calculation of the solution is still in progress. Please try again later.

The calculation of the solution has been aborted. Please return to the Create game tab and start a new game.

Traveling Salesperson Problem

1. introduction.

Traveling Salesperson Problem : TSP is a problem that tries to find a tour of minimum cost that visits every city once. In this visualization, it is assumed that the underlying graph is a complete graph with (near-)metric distance (meaning the distance function satisfies the triangle inequality) by taking the distance of two points and round it to the nearest integer.

2. Visualization

View the visualisation of TSP algorithm here.

Originally, all edges in the input graph are colored with the grey .

Throughout the visualization, traversed edge will be highlighted with orange .

There are two different sources for specifying an input graph:

• Draw Graph : You can put several points on the drawing box, but you must not draw any edge to ensure the (near-)metric property of the graph. After you have finished putting the points, the edges will be drawn automatically for you after.
• Example Graphs : You can select from the list of graphs to get you started.

4. Bruteforce

Bruteforce : It tries all (V-1)! permutation of vertices (not all V! since it does not matter where we start from). It enumerates all possibilities by doing a dfs search with parameters similar to those of Held-Karp algorithm, that is, the DFS search will return the value of the tour starting from current vertex to all vertices that we have not already visited.

Time complexity: O(V * (V - 1)!) = O(V!).

5. Dynamic Programming

Dynamic Programming : It uses a widely known algorithm called Held-Karp . In this visualization, it is implemented as a DFS search that is the same with the bruteforce algorithm, but with memoization to cache the answers. This dramatically brings down the run time complexity to O(2^V * V^2).

Time complexity: O(2^V * V^2).

Note that for N = 10, this algorithm takes roughly ~(100 * 2^10) = 102K operations while the bruteforce algorithm takes roughly ~(10!) = 3628800 operations, around 30 times faster.

6. Approximation

Approximation : There are two approximation algorithms available, a 2-approximation algorithm and a 1.5-approximation algorithm that is also well known as Christofides Algorithm.

Leveraging a Genetic Algorithm for Route Finding

Solving the traveling salesman problem with a genetic algorithm, applying genetic algorithms to the traveling salesman problem, shortest route in current generation, shortest route found, algorithm parameters.

An explanation of the algorithm parameters and implementation can be found here .

Instructions

• Press START to begin searching for shortest route between the default provided points.
• Algorithm parameters can be changed using the interface to the left.
• To run the algorithm against a custom set of points, click CLEAR and then click on the canvas to specify points.
• The app must be RESET before algorithm parameters are altered for the changes to take effect.

6   Traveling Salesman Problem

The traveling salesman problem (TSP) is a classic optimization problem in computer science and operations research. The problem can be stated as follows: given a set of cities and the distances between them, what is the shortest possible route that visits each city exactly once and returns to the starting city?

The TSP has many real-world applications, including logistics and transportation planning, circuit board drilling, and DNA sequencing. However, it is a well-known NP-hard problem, meaning that finding an optimal solution is computationally difficult for large instances of the problem. As a result, many heuristic and approximation algorithms have been developed to find suboptimal solutions that are still very good in practice. In this chapter, we present several mathematical formulations of the TSP existing in the literature and implement them using OR-Tools.

6.1 TSP Instances

Before discussing the mathematical models of the TSP, we first provide an introduction to the instances that will be utilized to test various formulations and illustrate the resulting TSP solutions. The TSP is a widely recognized optimization problem that has been studied for several decades. Due to its significance, many benchmarking problem instances of varying sizes are available in literature. In this chapter, we do not aim to solve the most challenging TSP instances, but instead, our objective is to demonstrate how to apply different formulations of the TSP using OR-Tools.

To achieve this objective, we will focus on presenting some of the small-sized instances that can be solved effectively using OR-Tools. These instances are well-documented, which makes them easy to understand and implement in practice. Additionally, they help illustrate the optimization techniques used to solve the TSP, such as branch-and-bound and cutting plane methods. Moreover, small-sized instances allow for quicker computation, making it easier to observe the behavior of different algorithms and identify which formulations are most efficient.

By presenting a range of examples, we aim to provide a clear understanding of how to implement different TSP formulations using OR-Tools, which can be applied to real-world problems in various domains, such as transportation planning and logistics, network design, and circuit board drilling. Additionally, we aim to demonstrate the advantages and limitations of different TSP formulations and algorithms, highlighting which techniques perform well under specific circumstances. By doing so, readers can gain insight into how to apply TSP optimization techniques to their own problems effectively.

6.1.1 TSPLIB

The TSP instances used in this section are sourced from TSPLIB95 , a library of TSP benchmark instances. To make it easier to work with these instances, we utilize the tsplib95 Python library, which can be installed using the pip install tsplib95 command.

In the code snippet below, we demonstrate how to use the tsplib95 package to load the ulysses22.tsp problem from a data file downloaded from TSPLIB95. The loaded data can be used to formulate and solve TSP instances using OR-Tools or other optimization tools. The full instance data is provided at the end for reference. By leveraging the tsplib95 package, we can quickly and easily access TSP instances for experimentation and analysis, and focus our efforts on the formulation and optimization aspects of the problem.

The list of nodes can be retrieved using the get_nodes() function, as shown below.

To get the distance between any pair of nodes, we use the get_weight() function.

6.1.2 Visualize TSP Solution

In this section, our goal is to gain a better understanding of the TSP problem by visualizing the optimal solution found for instances provided by TSPLIB95. To achieve this, we define a class called TspVisualizer in our code that is responsible for displaying the route that connects all nodes in a TSP solution. The TspVisualizer class contains a single function, called show(locations, edges) , which accepts two input parameters: locations and edges .

The locations parameter is a dictionary that contains the mapping between location ID and its corresponding coordinates. The edges parameter is a list of edges that form the TSP tour. By calling the show function with the appropriate input parameters, we can visualize the TSP tour and gain an intuitive understanding of what the TSP problem is trying to accomplish. This visualization can be a helpful tool in understanding how the different TSP formulations and algorithms work, and can aid in identifying potential improvements to the solution. The use of the TspVisualizer class allows for easy visualization of the TSP solution and makes it possible to explore and analyze TSP instances in a more meaningful way.

Now let’s load the optimal solution for the aforementioned instance and show its content below.

The code snippet below plots the optimal tour, which is shown in Figure  6.1 .

Let’s put this visualization procedure into a dedicated function, as is given below.

Figure  6.2 and Figure  6.3 show the optimal tours for the berlin52 and pr76 instances, respectively.

6.2 Problem Description

Let \(\mathcal{G} = (\mathcal{V}, \mathcal{A})\) be an undirected complete graph, where \(V = \{1, 2, \cdots, n\}\) represents a set of \(n\) cities or vertices, and \(\mathcal{A} = \{(i, j)\ |\ i, j \in \mathcal{V}, i \neq j\}\) represents the set of edges connecting these cities. The edges in \(\mathcal{A}\) have weights or distances associated with them, \(c_{ij}\) , representing the distances or costs to travel between pairs of cities.

The objective of the TSP is to find the shortest possible closed tour that visits each city in \(\mathcal{V}\) exactly once and returns to the starting city, while obeying the following constraints:

• Each city must be visited exactly once: The tour must include all the cities in \(\mathcal{V}\) , and each city must be visited exactly once during the tour.
• The tour must be closed: The last city visited in the tour must be the same as the starting city, forming a closed loop.

6.3 Model 1 - DFJ

The first formulation was proposed by Dantzig, Fulkerson, and Johnson ( 1954 ) . It uses the following decision variables:

• \(x_{ij}\) : a binary variable that equals 1 if arc \((i, j) \in \mathcal{A}\) shows up in the optimal solution, 0 otherwise

We can state the model as follows:

\[\begin{align} \text{min.} &\quad \sum_{(i, j) \in \mathcal{A}} c_{ij} x_{ij} \label{tsp1-obj} \\ \text{s.t.} &\quad \sum_{j \in \mathcal{V},\ j \neq i} x_{ij} = 1, \ \forall i \in \mathcal{V} \label{tsp1-cons1} \\ &\quad \sum_{i \in \mathcal{V}, \ i \neq j} x_{ij} = 1, \ \forall j \in \mathcal{V} \label{tsp1-cons2}\\ &\quad \begin{split} & \sum_{i, j \in S, \ (i, j) \in \mathcal{A}} x_{ij} \leq |S| - 1,\\ &\qquad \forall S \subset \mathcal{V}, \ 2 \leq |S| \leq n - 2 \end{split} \label{tsp1-cons3} \\ &\quad x_{ij} \in \{0, 1\}, \ \forall (i, j) \in \mathcal{A} \label{tsp1-cons4} \end{align}\]

This specific TSP formulation aims to find the optimal route with the shortest total distance. To ensure that each node is visited exactly once, constraints \(\eqref{tsp1-cons1}\) and \(\eqref{tsp1-cons2}\) , also known as degree constraints , are used. Another set of constraints \(\eqref{tsp1-cons3}\) , called subtour elimination constraints, ensure that the solution does not contain any subtours. Subtours are smaller cycles within the larger route that violate the requirement of visiting each city exactly once. Two examples of solutions with subtours are shown in figures Figure  6.4 and Figure  6.5 . While these solutions satisfy the degree constraints, they violate the subtour elimination constraints. A subtour contains the same number of edges (or arcs) as nodes, so limiting the number of edges to be less than the number of nodes can help to eliminate subtours. Furthermore, because of the presence of degree constraints, subtours with only one node cannot exist, and similarly, subtours with \(n-1\) nodes are also impossible. Therefore, it is acceptable to define the subtour elimination constraints only for subtours that contain between 2 and \(n-2\) nodes.

An equivalent way of constraints \(\eqref{tsp1-cons3}\) is

\[\begin{align} \sum_{i \in S}\sum_{j \notin S} x_{ij} \geq 1, \ \forall S \subset \mathcal{V}, \ 2 \leq |S| \leq n - 2 \label{tsp1-cons5} \end{align}\]

To understand this, observe that the value of \(|S|\) can be calculated as the sum of two terms: the sum of the decision variables \(x_{ij}\) for all edges \((i,j)\) that are included in the subset, and the sum of the decision variables \(x_{ij}\) for all edges that cross the boundary of the subtour, that is, \(|S| = \sum_{i, j \in S, \ (i, j) \in \mathcal{A}} x_{ij} + \sum_{i \in S}\sum_{j \notin S} x_{ij}\) . This means that the constraints \(\eqref{tsp1-cons3}\) and \(\eqref{tsp1-cons5}\) are interchangeable, as they represent the same condition in different forms.

To simplify the implementation of different TSP formulations that will be presented in the following sections, we have created a base class called TspModel in the code below. This class contains the instance information that needs to be solved, as well as several helper functions. Within the class definition, the attribute _node_list holds the list of nodes that must be visited by the TSP tour. The attribute _node_coords is a dictionary that stores the location information for each node. Finally, the attribute _distance is another dictionary that provides the distance between any pair of nodes. The read_inputs() function, defined between lines 15 and 31, takes a TSP problem instance and extracts the necessary information for solving the problem later. The get_combinations() function, defined between lines 33 and 34, generates all possible combinations of nodes with the specified size.

To implement the TSP model using OR-Tools, we define the TspModelV1 class that inherits from the base class TspModel . The constructor initializes a solver object and defines attributes to store decision variables and the optimal solution. The _create_variables() function creates binary decision variables for every arc in the problem, while the _create_objective() function calculates the total traveling cost. Degree constraints are defined in the _create_degree_constraints() function, while the subtour elimination constraints are defined in the _create_subtour_elimination_constraints() function. The build_model() function needs to be called before optimize() to construct the model.

Now we use the TspModelV1 class to solve the burma14 instance and plots the optimal solution found by the OR-Tools in Figure  6.6 .

6.4 Model 2 - MTZ

In this formulation, an alternative way of modeling the subtour elimination constraints was proposed by Miller, Tucker, and Zemlin ( 1960 ) . The model uses two types of decision variables:

• \(u_i\) : a continuous variable for \(i \in \mathcal{V} \backslash \{1\}\)

The complete formulation is given below.

\[\begin{align} \text{min.} &\quad \sum_{(i, j) \in \mathcal{A}} c_{ij} x_{ij} \label{tsp2-obj} \\ \text{s.t.} &\quad \sum_{j \in \mathcal{V},\ j \neq i} x_{ij} = 1, \ \forall i \in \mathcal{V} \label{tsp2-cons1} \\ &\quad \sum_{i \in \mathcal{V}, \ i \neq j} x_{ij} = 1, \ \forall j \in \mathcal{V} \label{tsp2-cons2}\\ &\quad \begin{split} &u_i - u_j + (n - 1) x_{ij} \leq n - 2, \\ &\qquad \forall i, j \in \{2, \cdots, n\}, i \neq j \end{split} \label{tsp2-cons3} \\ &\quad x_{ij} \in \{0, 1\}, \ \forall (i, j) \in \mathcal{A} \label{tsp2-cons4} \\ &\quad 1 \leq n_i \leq n - 1, i = 2, \cdots, n \label{tsp2-cons5} \end{align}\]

In this formulation, constraints \(\eqref{tsp2-cons1}\) and \(\eqref{tsp2-cons2}\) serve as the degree constraints requiring that there is only one arc entering and leaving a node. Constraints \(\eqref{tsp2-cons3}\) are the new subtour elimination constraints. To see how constraints \(\eqref{tsp2-cons3}\) effectively forbid subtours, let’s examine the example below in Figure  6.7 . In the figure, nodes 5 and 6 form a subtour and constraints \(\eqref{tsp2-cons3}\) become:

\[\begin{align} u_5 - u_6 + (7 - 1) * 1 \leq 7 - 2 \\ u_6 - u_5 + (7 - 1) * 1 \leq 7 - 2\\ \end{align}\]

which translate to:

\[\begin{align} u_5 \leq u_6 - 1 \\ u_6 \leq u_5 - 1 \end{align}\]

\[\begin{align} u_5 & \leq u_6 - 1 \\ & \leq u_5 - 1 - 1\\ & \leq u_5 - 2 \end{align}\]

for which, we have \(0 \leq -2\) , which is obviously wrong. Therefore, any subtour will violate the constraints defined in \(\eqref{tsp2-cons3}\) .

The code below gives the complete program of the formulation. The new variable \(u_i\) is defined in function _create_variables() and the subtour elimination constraints are updated in function _create_subtour_elimination_constraints() .

We now use this formulation to solve the burma14 instance and show its optimal solution in Figure  6.8 .

Figure  6.9 shows the optimal solution found by the formulation for the ulysses22 instance.

6.5 Model 3 - Single Commodity Flow

The model uses two types of decision variables:

• \(y_{ij}\) : a continuous variable representing the flow on arc \((i, j) \in \mathcal{A}\)

\[\begin{align} \text{min.} &\quad \sum_{(i, j) \in \mathcal{A}} c_{ij} x_{ij} \label{tsp3-obj} \\ \text{s.t.} &\quad \sum_{j \in \mathcal{V},\ j \neq i} x_{ij} = 1, \ \forall i \in \mathcal{V} \label{tsp3-cons1} \\ &\quad \sum_{i \in \mathcal{V}, \ i \neq j} x_{ij} = 1, \ \forall j \in \mathcal{V} \label{tsp3-cons2}\\ &\quad y_{ij} \leq (n - 1) x_{ij}, \ \forall (i, j) \in \mathcal{A} \label{tsp3-cons3} \\ &\quad \sum_{j \in \mathcal{V}\backslash \{1\}} y_{1j} = n - 1, \label{tsp3-cons4} \\ &\quad \sum_{i \in \mathcal{V}\backslash \{j\}} y_{ij} - \sum_{k \in \mathcal{V}\backslash \{j\}} y_{jk} = 1, \ \forall j \in \mathcal{V}\backslash \{1\} \label{tsp3-cons5}\\ &\quad x_{ij} \in \{0, 1\}, \ \forall (i, j) \in \mathcal{A} \label{tsp3-cons6} \\ &\quad y_{ij} \geq 0, \ \forall (i, j) \in \mathcal{A} \label{tsp3-cons7} \end{align}\]

In this formulation, the constraints \(\eqref{tsp3-cons3}\) - \(\eqref{tsp3-cons5}\) are the subtour elimination constraints. Specifically, constraints \(\eqref{tsp3-cons3}\) make sure that the amount of flow on any arc \((i, j)\) is at most \(n - 1\) when the arc is active. Constraints \(\eqref{tsp3-cons4}\) state that there is a total of \(n - 1\) flowing out of the source node 1. Constraints \(\eqref{tsp3-cons5}\) require that the incoming flow is 1 unit bigger than the outgoing flow at any node other than the source node 1. To see how this prevents subtours, we’ll use Figure  6.10 as an example.

According to constraints \(\eqref{tsp3-cons4}\) , we have the following relations:

\[\begin{align} v - w = 1 \\ w - v = 1 \end{align}\]

Summing them together leads to \(0 = 2\) , which is clearly false.

The code below gives the complete implementation of this formulation.

Figure  6.11 shows the optimal soution for instance burma14 found by this formulation.

Figure  6.12 shows the optimal route found by the formulation for the instance ulysses22 .

Figure  6.13 gives the optimal solution of instance berlin52 .

Figure  6.14 shows the optimal solution for instance pr16 .

6.6 Model 4 - Two Commodity Flow

The model uses three types of decision variables:

• \(y_{ij}\) : a continuous variable representing the flow of commodity 1 on arc \((i, j) \in \mathcal{A}\)
• \(z_{ij}\) : a continuous variable representing the flow of commodity 2 on arc \((i, j) \in \mathcal{A}\)

\[\begin{align} \text{min.} &\quad \sum_{(i, j) \in \mathcal{A}} c_{ij} x_{ij} \label{tsp4-obj} \\ \text{s.t.} &\quad \sum_{j \in \mathcal{V},\ j \neq i} x_{ij} = 1, \ \forall i \in \mathcal{V} \label{tsp4-cons1} \\ &\quad \sum_{i \in \mathcal{V}, \ i \neq j} x_{ij} = 1, \ \forall j \in \mathcal{V} \label{tsp4-cons2}\\ &\quad \sum_{j \in \mathcal{V}\backslash\{1\}} (y_{1j} - y_{j1}) = n - 1 \label{tsp4-cons3} \\ &\quad \sum_{j \in \mathcal{V}, j \neq i} (y_{ij} - y_{ji}) = -1, \ \forall i \in \mathcal{V} \backslash \{1\} \label{tsp4-cons4} \\ &\quad \sum_{j \in \mathcal{V}\backslash\{1\}} (z_{1j} - z_{j1}) = -(n - 1) \label{tsp4-cons5} \\ &\quad \sum_{j \in \mathcal{V}, j \neq i} (z_{ij} - z_{ji}) = 1, \ \forall i \in \mathcal{V} \backslash \{1\} \label{tsp4-cons6}\\ &\quad \sum_{j \in \mathcal{V} , j \neq i} (y_{ij} + z_{ij}) = n - 1, \ \forall i \in \mathcal{V} \label{tsp4-cons7}\\ &\quad y_{ij} + z_{ij} = (n - 1) x_{ij}, \ \forall (i, j) \in \mathcal{A} \label{tsp4-cons8} \\ &\quad x_{ij} \in \{0, 1\}, \ \forall (i, j) \in \mathcal{A} \label{tsp4-cons9} \\ &\quad y_{ij} \geq 0, \ \forall (i, j) \in \mathcal{A} \label{tsp4-cons10} \\ &\quad z_{ij} \geq 0, \ \forall (i, j) \in \mathcal{A} \label{tsp4-cons11} \end{align}\]

In this formulation, constraints \(\eqref{tsp4-cons3}\) - \(\eqref{tsp4-cons8}\) together serve as the subtour elimination constraints. To better understand the two commodity flow formulation, we’ll use Figure  6.15 as an example. At the source node 1, there is \(n-1\) units of commodity 1 leaving the node and there is no unit of commodity 2 leaving it. At each subsequent node, the amount of commodity 1 decreases by 1 unit while the amount of commodity 2 increases by 1 unit. On any arc in the tour, the total amount of commodities is always \(n - 1\) .

The code below gives the complete implementation of the two commodity flow formulation.

Figure  6.16 shows the optimals solution identified by the formulation for instance burma14 .

Figure  6.17 gives the optimal solution of the ulysses22 instance.

Figure  6.18 shows the optimals solution identified by the formulation for instance berlin52 .

6.7 Model 5 - Multi-Commodity Flow

• \(y_{ij}^k\) : a continuous variable representing the flow of commodity \(k\) on arc \((i, j) \in \mathcal{A}\) , \(k \in \mathcal{V} \backslash \{1\}\)

The complete formulation of the problem is presented below. To understand this formulation, let’s imagine that node 1 is the source node in the graph, and each of the remaining nodes demands one unit of different commodities. For instance, node 2 requires one unit of commodity 2, node 3 requires one unit of commodity 3, and so on. The problem can then be expressed as finding the most cost-effective graph that can handle the flow of all \(n-1\) commodities. Constraints \(\eqref{tsp5-cons1}\) and \(\eqref{tsp5-cons2}\) are the same as in other formulations. Constraints \(\eqref{tsp5-cons3}\) state that the arc connecting nodes (i,j) must be active to allow any commodity flow, essentially acting as a capacity constraint that limits the flow on the arc. Constraints \(\eqref{tsp5-cons4}\) indicate that exactly one unit of each commodity k flows out of the source node 1. Constraints \(\eqref{tsp5-cons5}\) require that no commodity flows into the source node 1. Constraints \(\eqref{tsp5-cons6}\) ensure that one unit of commodity k flows into node k, and constraints \(\eqref{tsp5-cons7}\) require that there is no flow of commodity k out of node k. Finally, constraints \(\eqref{tsp5-cons8}\) are flow conservation constraints that guarantee that the incoming flow is equal to the outgoing flow at all nodes except the source node for every commodity k.

\[\begin{align} \text{min.} &\quad \sum_{(i, j) \in \mathcal{A}} c_{ij} x_{ij} \label{tsp5-obj} \\ \text{s.t.} &\quad \sum_{j \in \mathcal{V},\ j \neq i} x_{ij} = 1, \ \forall i \in \mathcal{V} \label{tsp5-cons1} \\ &\quad \sum_{i \in \mathcal{V}, \ i \neq j} x_{ij} = 1, \ \forall j \in \mathcal{V} \label{tsp5-cons2}\\ &\quad y_{ij}^k \leq x_{ij}, \ \forall (i, j) \in \mathcal{A}, k \in \mathcal{V} \backslash \{1\} \label{tsp5-cons3}\\ &\quad \sum_{j \in \mathcal{V} \backslash \{1\}} y_{1j}^k = 1, \ \forall k \in \mathcal{V} \backslash \{1\} \label{tsp5-cons4} \\ &\quad \sum_{j \in \mathcal{V} \backslash \{1\}} y_{j1}^k = 0, \ \forall k \in \mathcal{V} \backslash \{1\} \label{tsp5-cons5} \\ &\quad \sum_{j \in \mathcal{V} \backslash \{k\}} y_{jk}^k = 1, \ \forall k \in \mathcal{V} \backslash \{1\} \label{tsp5-cons6} \\ &\quad \sum_{j \in \mathcal{V} \backslash \{k\}} y_{kj}^k = 0, \ \forall k \in \mathcal{V} \backslash \{1\} \label{tsp5-cons7} \\ &\quad \sum_{i \in \mathcal{V} \backslash \{j\}} y_{ij}^k - \sum_{i \in \mathcal{V} \backslash \{j\}} y_{ji}^k = 0, \ \forall j, k \in \mathcal{V} \backslash \{1\}, j \neq k \label{tsp5-cons8} \\ &\quad x_{ij} = \{0, 1\}, \ \forall (i, j) \in \mathcal{A} \label{tsp5-cons9}\\ &\quad y_{ij} \geq 0, \ \forall (i, j) \in \mathcal{A}, k \in \mathcal{V} \backslash \{1\} \label{tsp5-cons10} \end{align}\]

6.8 Performance Comparison

We give in Table  6.1 the computational times required to find the optimal solutions for different instances. It is by no means a thorough or comprehensive performance comparison, as it is only based on one run and on a few instances. It can be seen from the table that the single commodity flow formulation seems to perform the best among all the five formulations.

• Latest Articles
• Top Articles
• Posting/Update Guidelines
• Article Help Forum

• View Unanswered Questions
• View All Questions
• View C# questions
• View C++ questions
• View Javascript questions
• View Visual Basic questions
• View Python questions
• CodeProject.AI Server
• All Message Boards...
• Running a Business
• Sales / Marketing
• Collaboration / Beta Testing
• Work Issues
• Design and Architecture
• Artificial Intelligence
• Internet of Things
• ATL / WTL / STL
• Managed C++/CLI
• Objective-C and Swift
• System Admin
• Hosting and Servers
• Linux Programming
• .NET (Core and Framework)
• Visual Basic
• Web Development
• Site Bugs / Suggestions
• Spam and Abuse Watch
• Competitions
• The Insider Newsletter
• The Daily Build Newsletter
• Newsletter archive
• CodeProject Stuff
• Most Valuable Professionals
• The Lounge  
• The CodeProject Blog
• Where I Am: Member Photos
• The Insider News
• The Weird & The Wonderful
• What is 'CodeProject'?
• General FAQ
• Ask a Question
• Bugs and Suggestions

Traveling Salesman Problem Visualization

Over the last 9 weeks I've had the pleasure of being enrolled in the Discrete Optimization course at Coursera taught by Pascal Van Hentenryck . I had previously taken several of other massive open online courses (MOOCs), but this was the most challenging and rewarding. The key ingredients of this course were the unquestionable enthusiasm by its instructor and assistants, who created an excellent series of lectures and were personally involved at every step, as well as a game-like grading system, where the better your algorithm, the better your grade. It was rather intense! None of the programming assignments are issued with a well-defined strategy for creating a solution. Instead, the lectures cover various types of techniques and tools to be implemented and tinkered with by the students. Another interesting feature of the course is that all of the lectures and assignments are available from the first day. Most courses impose a schedule of lectures and assignments to be watched and completed on a week-by-week basis. The open structure of Discrete Optimization had me feeling a bit bewildered at first. They do provide a suggested study plan, so I (mostly) stuck with that and was able to make steady progress throughout the course.

One of the topics that resonated with many of the students, myself included, was that of Local Search . It's an idea that's easy to conceptualize and program, yet very powerful. I implemented a Local Search solution for the Traveling Salesmen Problem and, along the way, added some code to visualize some of the larger solutions. It looked pretty cool to see so many points connected together by a continuous route. I began experimenting with animating the algorithm as it finds a solution. Later, the professor's assistant (AKA graciously-answering-forum-questions- Carleton Coffrin ) put out a call for the students to create visualizations of various heuristics that can be used to solve TSP. Here is my contribution – it displays Greedy algorithm , Local Search , and Simulated annealing strategies for a group of US cities.

• www.youtube.com/v/SC5CX8drAtU?hl=en_US&version=3&rel=0

I’ve seen some interest in knowing how this was created. Here are the steps:

• I wanted to use some "real" map data to help illustrate the problem.  From a list of cities from geonames.org , filtered by country and population to generate data sets
• Ran these through my TSP solver from the Discrete Optimization course assignment, collecting the intermediate routes as improvements are made
• Generated a metric ton of still images to illustrate the transitions between the routes - this involves:
• translating the points and lines onto a bitmap
• "tweening" many frames between each route to provide smooth transitions. I tried several different "easing functions" but ended up with something like "easeInOutQuad" shown on this Easing Functions page
• … also generate images for the distance and temperature
• Imported these as numbered frames into Adobe Premiere Elements - I don't use anything fancy, just the text, some cross-dissolve transitions, and alter the speed of the frames - the same could likely be done with open source editors ( VLMC ?)
• The map of the US is a "flat" Mercator projection so that the latitude and longitude coordinates from the city list will show up in approximately the correct location - it's from here: Mercator Projection.svg
• ... and then a bunch of slicing and dicing and mixing and matching inside the video editor to "tell the story"

The code was done in .NET – here’s some pseudo-code used to generate the animation:

This article, along with any associated source code and files, is licensed under The Code Project Open License (CPOL)

Comments and Discussions

Navigation Menu

Search code, repositories, users, issues, pull requests..., provide feedback.

We read every piece of feedback, and take your input very seriously.

Saved searches

Use saved searches to filter your results more quickly.

To see all available qualifiers, see our documentation .

travelling-salesman-problem

Here are 27 public repositories matching this topic..., jhackshaw / tspvis.

🗺️ Visualize and control algorithms for the traveling salesman problem

• Updated Jun 19, 2024

Carla-de-Beer / TSP-distance-calculator

Genetic Algorithm applied to to the Travelling Salesman Problem

• Updated Sep 7, 2023

clementreiffers / travelling-salesman-problem

Travelling Salesman Problem system in JavaScript with Functional Programming

• Updated Apr 1, 2023

AndrewB330 / TSP-Solver

Interactive travelling salesman problem solver. Branch & bound | Simulated annealing.

• Updated Nov 7, 2020

dioumedeiros-zz / genetic-algorithm

Resolução do problema do caixeiro viajante utilizando algoritmo genético

• Updated Jan 5, 2023

echoSTROMLOS / TSPwGA-Simulation

This project uses a Genetic Algorithm to find near-optimal solutions to the Traveling Salesman Problem (TSP). Users can visualize the evolving routes and compare them to the optimal solution found using Bruteforce.

• Updated Oct 25, 2023

anisantillans / traveling-avenge-.net

• Updated Apr 7, 2019

Abhi-tech-09 / AlgoVisualizer

It is an attempt to visualize various path-finding Algorithms.

• Updated May 28, 2021

ashayp22 / Traveling-Salesman-Genetic-Algorithm

solving the traveling salesman problem with genetic algorithms

• Updated Mar 12, 2020

vipul43 / fun_with_-p5.js-

making exciting web pages using p5 javascript library

• Updated Dec 13, 2022

b30wulffz / Visualizer-With-A-Twist

Visualization of algorithms in a clean user interface.

• Updated Nov 23, 2020

TristanBilot / genetic-travelling-salesman

Implementation of the travelling salesman problem using a genetic evolutionary approach

• Updated Feb 16, 2021

sanskarjaiswal2001 / Travelling-Salesman-Genetic-Algorithm

This is the improved version of the brute force approach which takes less time to give results for greater number of cities.

• Updated Jul 15, 2021

Axel-Jalonen / tsp.axelj.dev

A simple implementation of a nearest neighbours greedy algorithm to provide an answer to the travelling salesman problem.

• Updated Jul 1, 2024

d-lehel / algorithm-visualization

just a study project with p5.js

• Updated Nov 4, 2022

icimidemirag / tsp

BM218 algoritmalar ödevi içindir. Travelling salesman probleminin go.js ile görselleştirilmiş javascript çözümüdür.

• Updated Oct 30, 2022

sanskarjaiswal2001 / Travelling-salesman-lexicography

A project to visually solve the travelling salesman problem

• Updated Jul 17, 2021

rafaelMurata / rafaelmurata.github.io

• Updated Mar 9, 2018

DelSquared / Warframe-Cetus-Wisps-Travelling-Salesman-Problem

• Updated Nov 17, 2018

Lovely-Professional-University-CSE / int-246-project-Roll_No---A14_A24_B33_B60

int-246-project-Twinkle0799 created by GitHub Classroom

Improve this page

Add a description, image, and links to the travelling-salesman-problem topic page so that developers can more easily learn about it.

Curate this topic

Add this topic to your repo

To associate your repository with the travelling-salesman-problem topic, visit your repo's landing page and select "manage topics."

Traveling Salesman Problem Visualization

Over the last 9 weeks I've had the pleasure of being enrolled in the Discrete Optimization  course at taught by Pascal Van Hentenryck . I had previously taken several of other massive open online courses (MOOCs), but this was the most challenging and rewarding. The key ingredients of this course were the unquestionable enthusiasm by its instructor and assistants, who created an excellent series of lectures and were personally involved at every step, as well as a game-like grading system, where the better your algorithm, the better your grade. It was rather intense! None of the programming assignments are issued with a well-defined strategy for creating a solution. Instead, the lectures cover various types of techniques and tools to be implemented and tinkered with by the students. Another interesting feature of the course is that all of the lectures and assignments are available from the first day. Most courses impose a schedule of lectures and assignments to be watched and completed on a week-by-week basis. The open structure of Discrete Optimization had me feeling a bit bewildered at first. They do provide a suggested study plan, so I (mostly) stuck with that and was able to make steady progress throughout the course.

One of the topics that resonated with many of the students, myself included, was that of   Local Search . It's an idea that's easy to conceptualize and program, yet very powerful. I implemented a Local Search solution for the Traveling Salesmen Problem and, along the way, added some code to visualize some of the larger solutions. It looked pretty cool to see so many points connected together by a continuous route. I began experimenting with animating the algorithm as it finds a solution. Later, the professor's assistant (AKA graciously-answering-forum-questions- Carleton Coffrin ) put out a call for the students to create visualizations of various heuristics that can be used to solve TSP. Here is my contribution – it displays Greedy algorithm ,  Local Search , and Simulated annealing  strategies for a group of US cities.

I’ve seen some interest in knowing how this was created. Here are the steps:

• I wanted to use some "real" map data to help illustrate the problem.  From a list of cities from geonames.org , filtered by country and population to generate data sets
• Ran these through my TSP solver from the Discrete Optimization course assignment, collecting the intermediate routes as improvements are made
• translating the points and lines onto a bitmap
• "tweening" many frames between each route to provide smooth transitions. I tried several different "easing functions" but ended up with something like "easeInOutQuad" shown on this Easing Functions
• … also generate images for the distance and temperature
• Imported these as numbered frames into Adobe Premiere Elements - I don't use anything fancy, just the text, some cross-dissolve transitions, and alter the speed of the frames - the same could likely be done with open source editors ( VLMC ?)
• The map of the US is a "flat" Mercator projection so that the latitude and longitude coordinates from the city list will show up in approximately the correct location - it's from here: Mercator Projection.svg
• ... and then a bunch of slicing and dicing and mixing and matching inside the video editor to "tell the story"

The code was done in .NET – here’s some pseudo-code used to generate the animation:

REPORTS & PUBLICATIONS

• PODCASTS & VIDEOS
• REPORTS & PUBLICATIONS
• EVENTS CALENDAR

Academic Paper: The Travelling Salesman Problem

JUL 15 2024

Daniel Goldsmith, Senior Quantum Computing Technologist, and Joe Day-Evans, Quantum Computing Technologist at Digital Catapult , have authored a paper on the Travelling Salesman Problem (which is subject to peer review). They present a novel and more efficient formulation beyond the commonly used Quadratic Unconstrained Binary Optimisation (QUBO) and Higher Order Binary Optimisation (HOBO) approaches.  Their work used an ORCA PT-1 quantum boson sampler and demonstrated some promising results to more efficiently scale to larger networks compared to other approaches.

Read the paper

David Hall DPhil

Head of Delivery

Prof. Ian Walmsley is Chairman of the ORCA Computing Board and a leading figure in quantum optics, quantum memories and waveguide circuits. He is Provost of Imperial College, London, an Honorary Fellow at St Hugh's College, Oxford and a Fellow of the Royal Society, The Optical Society, the Institute of Physics and the American Physical Society. Previously, he was President of the Optical Society of America, Pro-Vice-Chancellor for Research and Innovation, Hooke Professor of Experimental Physics at the University of Oxford and Director of the NQIT (Networked Quantum Information Technologies) hub. Prof. Walmsley is recognised for developing the SPIDER technique for characterising ultra-fast laser pulses.